ЛейбницРефераты >> Математика >> Лейбниц
|
|
Как видно из чертежа, треугольники OHG и QQ"R подобны, откуда следует,
![]()
т. е. площадь прямоугольника Q'CDR' равна удвоенной площади треугольника OQR (с точностью до величины высшего порядка малости). Итак, если мы сопоставим точке на АВ, взятой между Q и R, точку между С и D на параллели из G к оси х и выполним такое построение для всех Δs, то в пределе получим кривую KLM, причем сектор ОАВО окажется составленным из бесконечно малых треугольников, площади которых - половины малых прямоугольников, составляющих площадь «под кривой KLM».
Тем самым доказано, что кривая KLM является, как выражались в XVII в., квадратрисой для кривой АВ. Термин квадратриса был тогда достаточно распространен: если рассматривалась квадратура
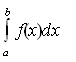
и удавалось подобрать кривую z=F(x) так, что
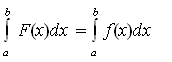
то вторая прямая была квадротисой для первой. Своеобразие результата Лейбница состояло, как было указано, в разбиении площади ОАВО на элементы прямыми, исходящими из одной и той же точки О. В общем же виде переход от кривой АВ к кривой KLM таков: если уравнение первой кривой в прямоугольных координатах есть y = f(x), где f(x) непрерывно дифференцируемая функция, то уравнение второй кривой будет
z(x)= f(x) -x f(x)'.
Лейбниц применил это преобразование к циклоиде и пришел к уже известным результатам. Новое он нашел, применяя свой прием к окружности. В соответствии с расположением осей, указанным на рис.2,
|
рис 2 |
Имеем уравнение окружности в виде y2=2ax-x2. И далее:
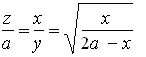
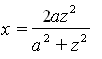
Квадратриса ОКМ в данном случае кривая, именуемая версиерой. Она показана на чертеже, на котором видны также ее точка перегиба (х = а/2, z = а/√З) и асимптота х = 2а. Площадь кругового сегмента а отсюда получается у Лейбница по следующей схеме (в записи которой использованы современные обозначения):
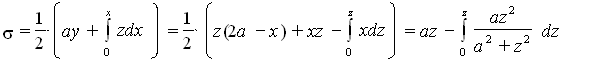
Далее Лейбниц преобразовывает подынтегральное выражение путем деления в степенной ряд и почленному интегрированию. Так для искомой площади получилось выражение:
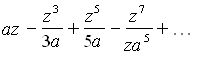
Отсюда при z= a (квадрант) получается то, что Лейбниц назвал арифметической квадратурой круга и что привело в восхищение Гюйгенса, - очень простого строения (правда, и очень плохой сходимости) ряд для π:
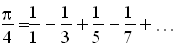
Лейбниц тут же получает с помощью этого выражения различные другие новые тогда соотношения. В частности, ряд для π/4 сразу дает при попарном объединении слагаемых:

В период с 1674 по 1675 год Лейбниц активно занимается алгеброй. Возможно ревность к занятиям алгебраическими вопросами, возникла после того как Лейбниц узнал о предложенном Ньютоном методе решения алгебраических уравнений с помощью логарифмических шкал. И здесь, конечно, он начинает размышлять об основной проблеме – получить формулы для решения алгебраических уравнений любой степени в радикалах, аналогичные тем, которые в XVI в. математикам итальянской школы удалось открыть для решения уравнений 3-й и 4-й степени. Попутно Лейбниц начинает заниматься частным вопросом, тогда тоже злободневным: было выяснено, что формула Тартальи - Кардано для уравнений третьей степени приводит к мнимым выражениям, когда корни уравнения вещественны («неприводимый случай»), но оставался неясным, так сказать, механизм этого странного явления, и общность формулы Тартальи - Кардано ставилась под сомнение. Об итоге алгебраических занятий Лейбница в 1674-1675 гг. можно судить по письму к Гюйгенсу написанному Лейбницем осенью 1675г.
Лейбниц утверждает в письме, что им впервые доказаны следующие результаты:
1) формулы Кардано вполне хороши и общи, извлекаются ли входящие в них корни или не извлекаются, получаются ли правильные значения (т. е. положительные) для корней уравнения или ложные (т. е. отрицательные);
2) радикалы четной степени, дающие решение уравнения, могут давать мнимости, и все-таки то обстоятельство, что они выражают действительные корни, может быть сделано, как выражается Лейбниц, осязательным без извлечения корней, чему пример формула:
![]()
3) всякое приводимое кубическое уравнение с рациональными коэффициентами имеет рациональный корень, что, конечно, дает возможность установить приводимость или неприводимость уравнения, не решая его. Эти результаты, продолжает Лейбниц, показывают, что можно безбоязненно применять иррациональные выражения в поисках решения уравнений высших степеней.
Все три основные положения, высказанные Лейбницем, верны, но доказательства подтверждающие их истинность отсутствовали а были только примеры, делающие правдоподобными сформулированные Лейбницем общие утверждения.
Но всё же основной вклад Лейбница в математическую науку был зделан в области математического анализа. И в этом свете хотелось бы рассмотреть статью Лейбница дотированную 25 октября 1675г. «Analysis Tetragonistica ex Centrobaricis» - «Анализ квадратур с помощью центров тяжестей». Эта статья выражала сравнительно давние размышления и Лейбница. В частности, в статье записано, что знание двух (статических) моментов фигуры относительно двух параллельных осей позволяет определить положение прямой, проходящей через центр тяжести фигуры, а по трем моментам относительно трех непараллельных осей можно определить и площадь фигуры и ее центр тяжести. Записывая в разных видах статические моменты, Лейбниц, в частности, приходит к следующему соотношению, которое приводится в его обозначениях:
omn. xω = ult. x∙omn. ω – omn. omn.ω.
Здесь omn. - начальные буквы латинского слова omnia, т. е. все, - обозначает объединение, суммирование «всех» бесконечно малых элементов, стоящих под этим знаком, х обозначает абсциссу точки на кривой, исходящей из начала координат, ω в этих выкладках Лейбница обозначает то элемент дуги (ds), то дифференциал ординаты (dy), ult.— начальные буквы латинского слова ultima (т. е. последняя) - относится к абсциссе. Итак, перед нами преобразование с помощью интегрирования по частям в такой примерно записи:
![]() (преобразование 1)
(преобразование 1)

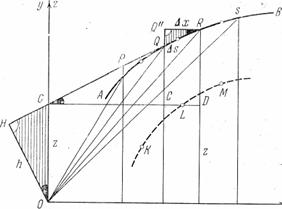 рис 1
рис 1