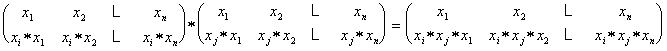Условимся о следующих обозначениях. Если A и B два подмножества группы G, то A*B обозначает множество всевозможных произведений элементов первого из них на элементы второго, а - множество всех обратных элементов из A. В этих обозначениях, например, условие, при котором A является подгруппой G можно записать в виде:

Определение

Пусть x некоторый фиксированный элемент группы G, а H - любая ее подгруппа. Множество x*H называется левым, а H*x - правым смежным классом группы по подгруппе.

Например, очевидно, что *H=H*=H, так что подгруппа Н сама является одним из смежных классов.

Свойства смежных классов

1. Отображение, определенное формулой является взаимно однозначным для всякого .

2. Каждый элемент x входит в смежный класс x*H.

3. Если y входит в смежный класс x*H , то y*H=x*H

4. Если y не входит в смежный класс x*H, то

(Свойства 1- 4 сформулированы для левых смежных классов, но аналогичными свойствами обладают и правые).

Доказательство.

1. сюръективно по определению смежного класса. Если, то есть , то по закону сокращения, то есть инъективно.

2. Поскольку входит в подгруппу H, x=x* входит в смежный класс x*H.

3. Пусть y=x*h и , то есть z= Тогда z=(x*h)* = x*(h*) и значит входит в класс x*H. Таким образом, . Обратное включение вытекает из того, что и значит входит в y*H.

4. Докажем от противного. Пусть классы x*H и y*H пересекаются и элемент z входит в каждый из них, так что . Тогда что противоречит нашему предположению.

Следствие

Если подгруппа H конечна, то все левые смежные классы содержат одинаковое число элементов, равное порядку этой подгруппы. (Следует из свойства 1.)

В качестве примера рассмотрим группу перестановок из 3 элементов. Составим для нее таблицу умножения. Эта группа состоит из 6 элементов .

Клетка таблицы, стоящая в i-ой строке и в j- ом столбце содержит номер элемента, равного . Она имеет следующий вид:

Рассмотрим подмножество H в состоящее из элементов и . (Будем писать: H={1,2}). Легко видеть, что H - подгруппа. (Заметим, что ). Пользуясь таблицей умножения находим левые смежные классы:

,,. Таким образом, имеем 3 различных левых смежных класса {1,2}, {3,4}, {5,6}. Аналогично строятся правые смежные классы: {1,2}, {3,5}, {4,6}.

Возьмем теперь {1,4,5}. - подгруппа четных перестановок . Для нее левые и правые смежные классы совпадают и состоят из элементов {1,4,5} и {2,3,6}.

Определение

Индексом [G:H] подгруппы H в группе G называется количество различных левых смежных классов G по H (если оно конечно).

Теорема Лагранжа

Если G конечная группа и H ее подгруппа, то

ord(G)={G:H]*ord(H)

(Здесь ord( ) обозначает порядок группы).

Доказательство

Пусть - полный перечень левых смежных классов G по H и класс содержит элементы . Тогда m - индекс [G:H] , а n - порядок H (по следствию из предыдущей теоремы). По свойству 3. все элементы попарно различны и по свойству 2. исчерпывают список элементов группы G. Значит, m*n=ord(G), что и требовалось.

Следствие

Порядок подгруппы делит порядок конечной группы.

В самом деле, число ord(G)/ord(H)=[G:H] является целым.

Замечания о таблицах умножения

Мы уже видели, что работая с конкретной конечной группой G, удобно иметь перед глазами ее таблицу умножения. Эта таблица называется таблицей Кэли. Ее можно построить для всякой АО на конечном множестве. Для этого элементы множества надо занумеровать: . В i- ой строке таблицы записываются элементы: . Заметим, что в случае, если АО превращает множество в группу G, все эти элементы попарно различны, как это вытекает из закона сокращения. Поскольку их число равно порядку G, каждая строка таблицы Кэли является некоторой перестановкой элементов группы . Например, если для группы условиться, что , первая строка будет тождественной перестановкой. Аналогично, перестановкой элементов группы будет и каждый столбец. В частности, таблица не имеет одинаковых строк или столбцов. Оказывается, что если элементу множества сопоставить i - ую строку таблицы Кэли, то произведению (произведение относительно АО !) , будет в случае, если АО ассоциативна, отвечать перестановка, равная произведению соответствующих перестановок. В самом деле, по правилу перемножения перестановок имеем: