Определение

Элементы коммутативной группы G называются ее системой образующих (с.о.) , если каждый элемент можно записать в виде: , где . Группа, имеющая систему образующих, называется группой с конечным числом образующих (г.к.о.)

Примеры.

1. Циклическая группа - группа с одной образующей.

2. Группа всех n-мерных векторов с целочисленными координатами с операцией сложения имеет стандартную с.о. e= , где - вектор, у которого единственная ненулевая координата - i ая , равная 1.

Отметим, что Z. Будем также считать, что - тривиальная группа.

3. Система {3,7} - является с.о. группы Z. Это вытекает из тождества: m= m*7+(-2m)*3 .

4. Всякая конечная абелева группа является г.к.о. так как за систему образующих можно взять, например, все элементы этой группы.

5. Группа Qрациональных чисел с операцией сложения не является г.к.о. В самом деле, если 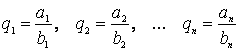- любые рациональные числа, записанные в виде отношения целых, то, приводя к общему знаменателю сумму , получим дробь, знаменатель которой не превосходит N= . Поэтому любая несократимая дробь с большим чем N знаменателем не является целочисленной линейной комбинацией данных рациональных чисел и они не образуют с.о.

Пусть G- группа с с.о. . Определим отображение формулой: 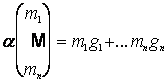. Очевидно, что является сюръективным гомоморфизмом. Будем называть стандартным гомоморфизмом для группы G c заданной с.о Он отображает стандартную с.о. группы в заданную с.о. группы G. Из существования стандартного гомоморфизма вытекает, что любая г.к.о. является гомоморфным образом группы . Отметим еще, что если - сюръективный гомоморфизм, то - с.о. группы K. Поэтому гомоморфный образ г.к.о. является г.к.о.

Теорема о подгруппах г.к.о.

Всякая подгруппа H группы G с с.о. допускает конечную с.о. , причем .

Доказательство.

Проведем индукцию по числу n образующих группы G . При n=1 G -циклическая группа и для нее теорема верна, так как всякая ее подгруппа циклична. Пусть для групп с (n-1) образующей теорема уже доказана; рассмотрим случай сформулированный в теореме. Определим множество

. Легко проверить, что - подгруппа и потому P=kZ, где . Если k>0 выберем так, чтобы . Пусть - подмножество G, состоящее из всевозможных линейных комбинаций , где все . Очевидно, что - подгруппа G с (n-1) образующей. Пусть также - подгруппа . По предположению индукции допускает конечную с.о. , где . Если k=0, и теорема доказана. Предположим, что k>0. Докажем тогда, что - с.о. подгруппы H. Пусть - произвольный элемент. Тогда h= . Значит,

=и потому=, откуда и теорема полностью доказана.

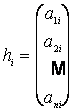Итак, любая подгруппа г.к.о. является г.к.о. Укажем удобный способ задания группы G с заданной с.о. с помощью матриц. Рассмотрим стандартный гомоморфизм . Тогда H=Ker- подгруппа г.к.о. и потому имеет конечную с.о. . Поскольку , можно записать: , где . Матрица с этими элементами полностью описывает подгруппу H, а, следовательно, и группу G.

Примеры.

1. Пусть G=- циклическая группа с образующей g. Стандартный гомоморфизм имеет ядро nZс образующей n. Здесь - (11) матрица (n).