Коммутативные группы с конечным числом образующих

Рефераты >> Математика >> Коммутативные группы с конечным числом образующих

Как было показано на предыдущей лекции, каждая г.к.о. G с n образующими задается (n m) матрицей , причем эквивалентные матрицы определяют одинаковые группы. Будем называть прямоугольную матрицу А диагональной , если все ее элементы =0 при i j. Последовательно перечисляя ее диагональные элементы, будем записывать такую матрицу в виде: A=diag().

Теорема о приведении матрицы к диагональному виду.

Всякая целочисленная прямоугольная матрица А эквивалентна диагональной матрице diag(), с положительными , причем все числа - целые.

Доказательство.

Для нулевой матрицы теорема очевидно верна. Будем считать, что А0. Выберем из множества ненулевых элементов А любой из наименьших по модулю и назовем его главным элементом А. Абсолютная величина главного элемента будет обозначаться h(A). Таким образом для любого ненулевого элемента этой матрицы .

Лемма

Существует матрица эквивалентная А, все элементы которой кратны ее главному элементу.

Доказательство леммы.

Выберем среди всех матриц эквивалентных А ту матрицу , у которой h() минимально. Покажем, что эта матрица удовлетворяет условию, указанному в лемме. Проведем доказательство от противного. Пусть - главный элемент этой матрицы так что . Допустим, что некоторый элемент этой матрицы не делится на нацело и придем к противоречию. Рассмотрим 3 случая. Пусть сначала p=i, то есть выбранные элементы расположены в одной строке. Разделим на с остатком: , где . Вычитая из q-ого столбца j-ый с коэффициентом s, придем к эквивалентной матрице , у которой h()r<h(), что противоречит выбору матрицы . Если p i, но q=j, то можно произвести аналогичное преобразование строк матрицы, что опять приведет нас к противоречию. Пусть, наконец, все элементы i-ой строки и все элементы j-ого столбца кратны , но не делится на главный элемент нацело. Пусть k=. Вычитая из p-ой строки ее i-ую строку с коэффициентом (k-1) придем к эквивалентной матрице , у которой и элемент не делится на нацело. Имеем: h()=h(A). Строгое неравенство приводит к противоречию; если же имеет место равенство, мы получаем первый случай и снова впадаем в противоречие. Лемма доказана.

Доказательство теоремы будем проводить индукцией по n. При n=1 утверждение теоремы очевидно. Пусть теорема уже доказана для матриц с (n-1) строкой. Рассмотрим матрицу А с n строками. Выберем для нее эквивалентную матрицу , удовлетворяющую условиям леммы. Пусть . Переставляя строки и столбцы и если надо умножая ее строку на -1, приходим к эквивалентной матрице , у которой . Вычитая теперь из каждой строки ее первую строку с подходящим коэффициентом и проделывая аналогичные операции с ее столбцами, приходим к матрице, у которой все элементы первой строки и первого столбца равны 0 за исключением первого элемента, равного , причем все элементы этой матрицы кратны . Применяя предположение индукции к матрице , полученной вычеркиванием первой строки и первого столбца, мы и завершаем доказательство теоремы.

Пример.

(стрелками обозначены э.п. строк и столбцов)

.

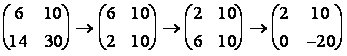
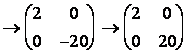Опишем теперь структуру группы G с с.о. , для которой =diag() , причем мы считаем, что По построению G=, где H- подгруппа с с.о. {}. Пусть -циклическая подгруппа G. Очевидно, ( при i>r). Каждый элемент однозначно представляется в виде суммы: , где 0< при i=1,2, .r и при i>r .