Математическая Логика

Рефераты >> Математика >> Математическая Логика

2.1.2 Декартова степень произвольного множества.

Опр: - множество всевозможных упорядоченных наборов длины n , элементов множества А.

2.1.3 Определение булевой функции от n переменных.

Любое отображение - называется булевой функцией от n переменных, притом множество

2.1.4 Примеры булевой функции.

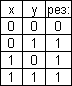
1) логическая сумма (дизъюнкция).

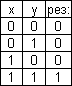
2) логическое умножение (конъюнкция).

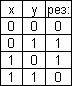
3) сложение по модулю два.

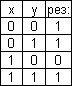
4) логическое следствие (импликация).

5) отрицание.

2.1.5 Основные булевы тождества.

1) (ассоциативность)

2) (коммутативность)

3) (свойство нуля)

4) (закон поглощения для 1)

5) (ассоциативность)

6) (коммутативность)

7) (свойство нуля по умножению)

8) (свойство нейтральности 1 по умножению)

9) (дистрибутивность)

10) (дистрибутивность 2)

11) (закон поглощения)

12) ( Законы

13) де Моргана)

14) (закон снятия двойного отрицания)

15) (tertium non datur – третьего не дано)

16) (ассоциативность)

17)

18)

19)

20)

21) (Свойства

22) идемпотентности)

2.2 Дизъюнктивные нормальные формы.

2.2.1 Основные определения.

- конечный алфавит из переменных.

Рассмотрим слово:

Экспоненциальные обозначения:

- элемент конъюнкции.

S – длина элемента конъюнкции.

ДНФ – дизъюнкция нескольких различных элементарных конъюнкций.

Любая булева функция может быть представлена как ДНФ

2.2.2 Теорема о совершенной ДНФ.

Любая булева функция тождественно не равная 0 может быть разложена в ДНФ следующего вида:

Опр: Носитель булевой функции

.

Лемма:

1) это элементарно

2) возьмем набор

а)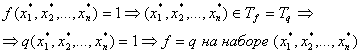

б)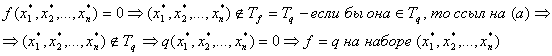

Доказательство: , будем доказывать, что.

1) Докажем, что . Возьмем он попадает в число суммируемых наборов и по нему будет проводиться сумирование.

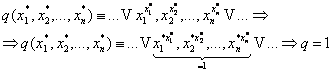
2) Докажем, что . Возьмем другой набор из

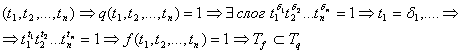
Следовательно

2.2.3 Некоторые другие виды ДНФ.

Опр: - называется минимальной ДНФ, если она имеет - наименьшую возможную длину из всех ДНФ данной функции.

Опр: - называется тупиковой ДНФ, если из неё нельзя выбросить ни одного слагаемого с сохранением булевой функции.

(Легко понять, что любая минимальная ДНФ является тупиковой, а обратное не верно.)

Опр: К-мерной гранью называется такое подмножество , которая является носителем некоторой элементарной конъюнкции длины: n-k.