Инбридинг

Рефераты >> Математика >> Инбридинг

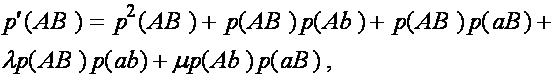
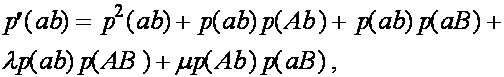
(3)

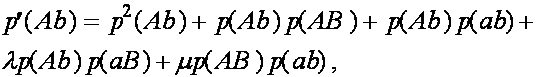
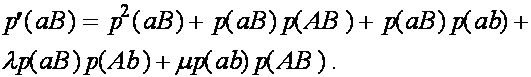
Дадим комментарии к правой части первой формулы (остальные формулы выписываются аналогично). Первое слагаемое - частота генотипа (AB)(AB). При мейозе каждая особь данного генотипа с единичной вероятность порождает гаметы (AB). Второе слагаемое - половинная частота генотипа (AB)(Ab). В силу сделанного выше замечания, несмотря на кроссиговер, каждая особь этого генотипа с вероятностью при мейозе дает гаметы (AB) и (Ab) (нас в данном случае интересуют гаметы (AB)). Совершенно аналогично, отражает вклад генотипа (AB)(aB) в образование гамет (AB). Четвертое слагаемое выписывается из следующих соображений. При условии, что кроссинговер не произошел (вероятность ), особь генотипа (AB)(ab) с вероятностью даст гамету (AB). Частота генотипа (AB)(ab) суть . Обратимся к последнему слагаемому. При условии кроссинговера (вероятность ) особь генотипа (Ab)(aB) (частота ) с вероятностью порождает гамету (AB) (см. рисунок выше). Осталось заметить, что кроссинговер ни в каком другом генотипе не может привести к появлению гаметы (AB).

Преобразуем формулы (3). Выкладки проведем на примере первой формулы. Подставляя , получим

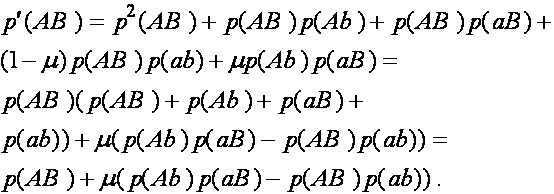Здесь учтено, что . Введем обозначение В результаты преобразований формулы (3) приобретают вид:

(4)

Величина называется мерой неравновесности состояния (если , то частоты гамет постоянны). Рассмотрим эволюцию . В силу (4) имеем:

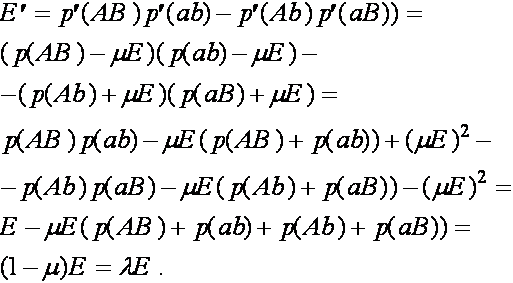
Итак

. (5)

Проследим за эволюцией частот , , , (нижний индекс - номер поколения). В силу (4) и(5)

(6)

.

Это система так называемых разностных уравнений. Она решается следующим образом. Выписывается матрица правых частей уравнений:

.

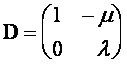Находятся ее собственные значения и . Матрица - диагональная, поэтому , . Собственные векторы (нетривиальные решения систем ) суть

, .

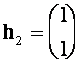При вычислении использовано равенство: . Система резностных уравнений (6) имеет два линейно независимые решения: и . Общим решением является их линейная комбинация:

.

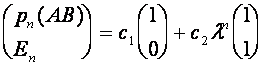Константы и определяются из начального условия (при ):

.

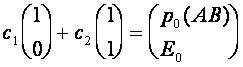Получаем и . В результате получаем решение системы (6):

,

.

Совершенно аналогично исследуется изменение частот гамет (ab), (Ab), (aB):

,

,

.

Из полученных формул следует, что при (с ростом номера поколения) и

, , , .

Тем самым, частоты гамет стремятся к состоянию равновесия, которое не достижимо за конечное число поколений. Частоты генотипов определяются через частоты гамет, а, следовательно, также стабилизируются. В отличии от случая, соответствующего закону Харди -Вайнберга, стабилизация в первом поколении не наступает.

Как уже говорилось, начальное состояние равновесно, т.е. частоты гамет в дальнейшем не меняются, если , т.е.

.

Исследуем условия равновесности. Рассмотрим частоты генов