Возрастание средней приспособленностиРефераты >> Математика >> Возрастание средней приспособленности
Выше средней приспособленностью в n -ом поколении была названа величина 
. Она интерпретировалась, как полная вероятность того, что особь n -ого поколения доживает до этапа размножения. Покажем, что средняя приспособленность -неубывающая функция от номера поколения n. Таким образом, эволюция происходит в сторону возрастания приспособленности популяции, что полностью соответствует теории Ч. Дарвина.
Запишем 
как функцию от 
:
и вычислим ее производные:
,
.
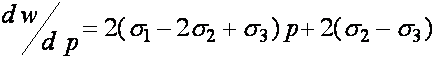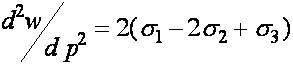Таким образом, экстремальное значение достигается при
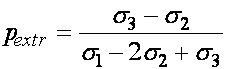(23)
и является максимумом при 
и минимумом, если 
.
Рассмотрим первый случай, когда 
. Квадратичная функция не имеет экстремума на интервале 
. Действительно, пусть для определенности 
. Тогда из (23) следует, что экстремальная точка 
. Для всего интервала производная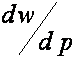 
имеет один и тот же знак. При 
имеем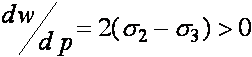 
. Следовательно, функция на интервале монотонно растет. Напомним, что в рассматриваемом случае для траектории 
отображения 
также монотонно 
при 
. В результате 
. При этом 
.
Второй случай 
подобен первому. Функция на интервале не имеет экстремума и монотонно убывает. Согласно полученным ранее результатам, для траектории отображения имеем: 
. В результате последовательность 
оказывается монотонно растущей: 
. При этом 
при .
В третьем случае (
, ) экстремальная точка 
является точкой максимума, т.к.
.
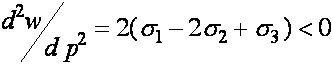На интервале 
функция монотонна растет, а на интервале 
монотонно убывает. Одновременно, точка 
, согласно (18), является устойчивым состоянием равновесия 
(состояние полиморфизма). Как показано выше, если начальная точка траектории 
, то для всех ее точек 
. Тем самым, последовательность монотонно растет. Если же начальная точка 
, то . Тем не менее, последовательность по-прежнему монотонно растет, в силу монотоного убывания функции на соответствующем интервале.
Четвертый случай (
, 
) аналогичен предыдущему. Состояние неустойчивого полиморфизма является точкой минимума для средней приспособленности. Траектории (последовательности ) с начальными условиями 
монотонно убывают. Одновременно, на соответствующем промежутке также монотонно убывает функция . В результате последовательность монотонно растет. Если же 
, то последовательность монотонно растет, а вместе с ней и последовательность , т.к. функция для 
монотонно растет.
Рисунок иллюстрирует направление поведение средней приспособленности в рассмотренных случаях.
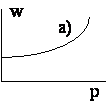
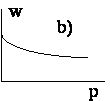
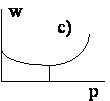
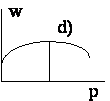
Отметим, что возрастание средней приспособленности можно доказать непосредственно, не разбирая в отдельности каждый случай. Далее, поскольку средняя приспособленность есть ограниченная величина, можно сделать вывод, что последовательность <
имеет предел при . Используя этот">