СП классифицируются по видам состояний и аргументу t. При этом СП могут быть с дискретными или непрерывными состояниями или временем. Например, любой выборочный контроль продукции будет относиться к СП с дискретными состояниями (- годная, - негодная продукция) и дискретным временем (, - времена проверки). С другой стороны, случай отказа любой машины можно отнести к СП с дискретными состояниями, но непрерывным временем. Проверки термометра через определенное время будут относиться к СП с непрерывным состоянием и дискретным временем. В свою очередь, например, любая осциллограмма будет записью СП с непрерывными состояниями и временем.

Кроме указанных выше примеров классификации СП существует еще одно важное свойство. Это свойство описывает вероятностную связь между состояниями СП. Так, например, если в СП вероятность перехода системы в каждое последующее состояние зависит только от предыдущего состояния, то такой процесс называется процессом без последействия (рис.1).

Зависимость называют переходной вероятностью, часто говорят, что именно процесс без последействия обладает марковским свойством, однако, строго говоря, здесь есть одна неточность. Дело в том, что можно представить себе СП, в котором вероятностная связь существует не только с предшествующими, но и более ранними () состояниями, т.е.

(1)

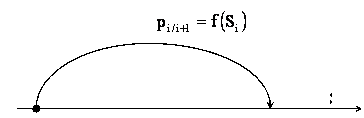Рис. 1. Схема процесса без последействия

Такие процессы также рассматривались А.А. Марковым, который предложил называть их в отличие от первого случая (простой цепи) - сложной цепью. В настоящее время теория таких цепей разработана слабо и обычно применяют так называемый процесс укрупнения состояний путем математических преобразований, объединяя предшествующие состояния в одно.

Это обстоятельство должно обязательно учитываться при составлении математических моделей принятия решений.

Выше мы совершили незаметный терминологический переход от понятия СП к “марковской цепи”. Теперь эту неясность следует устранить. Отметим, во-первых, что случайный процесс с дискретными состояниями и временем называется случайной последовательностью.

Если случайная последовательность обладает марковским свойством, то она называется цепью Маркова.

С другой стороны, если в случайном процессе состояния дискретны, время непрерывно и свойство последействия сохраняется, то такой случайный процесс называется марковским процессом с непрерывным временем.

Марковский СП называется однородным, если переходные вероятности остаются постоянными в ходе процесса.

Цепь Маркова считается заданной, если заданы два условия.

1. Имеется совокупность переходных вероятностей в виде матрицы:

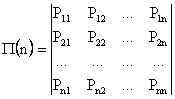. (2)

2. Имеется вектор начальных вероятностей

, … (3)

описывающий начальное состояние системы.

Матрица (2) называется переходной матрицей (матрицей перехода). Элементами матрицы являются вероятности перехода из i-го в j-е состояние за один шаг процесса. Переходная матрица (2) обладает следующими свойствами:

a) , (3a)

б) .

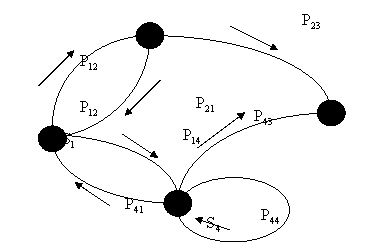
Матрица, обладающая свойством (3a), называется стохастической. Кроме матричной формы модель марковской цепи может быть представлена в виде ориентированного взвешенного графа (рис. 2).

Рис. 2. Ориентированный взвешенный граф

Вершины графа обозначают состояние , а дуги- переходные вероятности.

Множество состояний системы марковской цепи, определенным образом классифицируется с учетом дальнейшего поведения системы.

1. Невозвратное множество (рис. 3).

Рис. 3. Невозвратное множество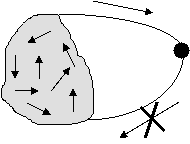

В случае невозвратного множества возможны любые переходы внутри этого множества. Система может покинуть это множество, но не может вернуться в него.

2. Возвратное множество (рис. 4).

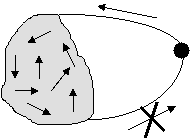Рис. 4. Возвратное множество

В этом случае также возможны любые переходы внутри множества. Система может войти в это множество, но не может покинуть его.

3. Эргодическое множество (рис. 5).

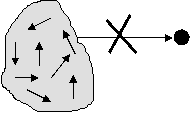Рис. 5. Эргодическое множество

В случае эргодического множества возможны любые переходы внутри множества, но исключены переходы из множества и в него.

4. Поглощающее множество (рис. 6)

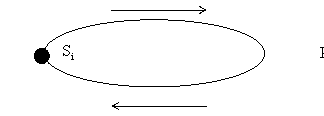Рис. 6. Поглощающее множество

При попадании системы в это множество процесс заканчивается.

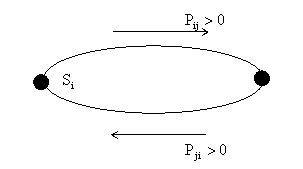
Кроме описанной выше классификации множеств различают состояния системы:

а) существенное состояние (рис.7): возможны переходы из в и обратно.