О некоторых применениях алгебры матрицРефераты >> Математика >> О некоторых применениях алгебры матриц
Оглавление
Введение
§1. О правиле Крамера
§2. Применение циркулянтов малых порядков в теории чисел
§3. Матричный вывод формулы Кардано
Литература
§1. О правиле Крамера
В литературе известны разные способы решения Крамеровой системы линейных алгебраических уравнений. Один из них – матричный способ – состоит в следующем.
Пусть дана Крамерова система, т.е. квадратная система 
линейных уравнений с неизвестными 
(1)
Определитель которой отличен от нуля:
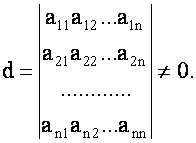(2)
Систему (1) можно представить в виде одного матричного уравнения
(3)
где 
- матрица коэффициентов при неизвестных системы (1),
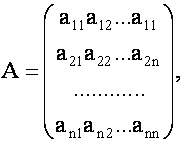(4)
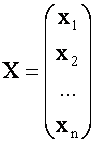- столбец (Матрица-столбец) неизвестных
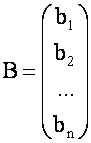- столбец свободных членов системы (1)
Так как 
, то матрица невырожденная и для нее существует обратная матрица 
. Умножив равенство (3) на (слева), получим (единственное) решение системы в следующей матричной форме (в предположении, что она совместима и 
- ее решение)
,
где обратная матрица имеет вид:
(
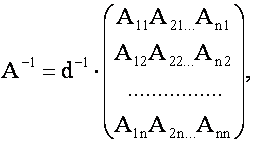
-алгебраическое дополнение элемента 
в определителе 
)
Другой известный способ можно назвать методом алгебраических дополнений. Его использование предполагает владение понятием алгебраического дополнения как и в матричном способе, теоремой о разложении определителя по столбцу (строке), теоремами о замещении и об аннулировании.
Предлагаемый нами новый метод опирается на теорему Коши-Бине об определителе произведения матриц.
Суть этого метода можно понять легко, если сначала рассмотрим случай 
. Очевидно, что при выполняются следующие матричные равенства (если задана система (1)):
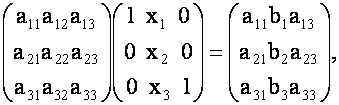
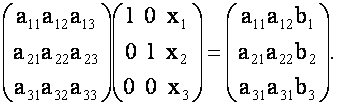
Переходя к определителям в этих равенствах и обозначив определители правых частей соответственно через 
получим формулы Крамера:
(
)
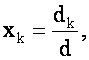
(Правило Крамера)
Переход к общему случаю Крамеровых систем (1) порядка 
ничего по существу не меняет. Просто следует заметить, что матрица 
с определителем 
получается из единичной матрицы заменой 
-го столбца столбцом неизвестных:
(5)
Теперь из равенств
,
где 
- матрица, получающаяся заменой - го столбца матрицы столбцом свободных членов системы (1), причем к формулам Крамера, взяв определители от обеих частей в каждом равенстве:
, откуда ввиду имеем
.
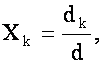
(здесь 
получается из , как и из ).
Другой, еще более короткий способ отыскания решения системы (1) состоит в следующем (по-прежнему ): пусть система (1) совместна и числа (после переобозначений) образуют ее решение. Тогда при 
имеем, используя два линейных свойства определителя:
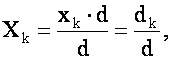
Можно начать и с определителя , в котором вместо свободных членов в -м столбце подставлены их выражения согласно (1); используя соответствующие свойства определителя, получим:
(),
откуда и получаются формулы Крамера.
Замечание. Проверка того, что значения неизвестных, определяемые по формуле Крамера удовлетворяют системе (1), (т.е. образуют решение системы), производится одним из известных способов.
