Гидравлика
Движение воды в русле канала.
Открытые русла могут быть естественными или искусственными.
К естественным открытым руслам относятся реки и ручьи, к искусственным– каналы, безнапорные трубы (например, дренажные),гидротехнические тунели и т. д.
Особенность движения в открытом русле заключается в том, что поток здесь ограничен не со всех сторон, а имеет свободную поверхность, все точки которой находятся под воздействием одинакового внешнего давления (атмосферного). Равномерное движение жидкости в открытых каналах или в трубопроводах с частично заполненным поперечным сечением устанавливается, когда геометрический уклон трубопровода или дна канала имеет постоянное значение по всей длине и форма поперечного сечения не меняется. Шероховатость стенок канала также должна иметь постоянное значение.
При отмеченных условиях возможно существование равномерного движения. Однако для реализации равномерного движения необходимо еще, чтобы поперечное сечение потока в канале было также постоянным по всей длине канала.
Следует отметить, что безнапорное движение воды представляет значительно более сложное явление по сравнению с напорным движением, так как наличие свободной поверхности потока приводит к изменению площадей живых сечений по длине последнего даже при незначительных препятствиях. Это требует рассмотрения процессов волно–образования, заставляет в некоторых случаях считаться с влиянием сил поверхностного натяжения и т. п.
При гидравлических расчетах открытых каналов и безнапорных трубопроводов ставится задача определения скорости движения жидкости в канале, площади сечения и наивыгоднейшей формы канала.
При равномерном движении жидкости в открытом русле гидравлический iг и пьезометрический iп уклоны, а также уклон дна русла iп равны между собой:
iг = iп = iд (5. 29)
С учетом равенства (5. 29) открытые каналы и безнапорные трубопроводы рассчитываются по формулам, которые были выведены ранее для напорных трубопроводов (формулы Шези и Павловского). Значения коэффициента шероховатости п для широкого диапазона условий приведены в приложении 2.
Как следует из формулы Шези, канал будет обладать наивыгоднейшей формой, если при заданной площади поперечного сечения он будет иметь наименьший смоченный периметр. При этом канал будет обеспечивать наибольший расход. Наиболее выгодными профилями каналов являются круг и полукруг. На практике чаще применяются каналы трапецеидальной формы, поскольку в грунте полукруглое сечение достаточно трудно.
Более подробные сведения о движении воды в открытых руслах можно почерпнуть в специальной литературе.
Местные сопротивления
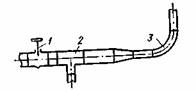
При движении реальной жидкости помимо потерь на трение по длине потока могут возникать и так называв мые местные потери напора. Причина последних, например в трубопроводах, – разного рода конструктивные вставки: колено 3, тройники 2, сужения и расширения трубопровода, задвижка 1, вентили и т. п., необходимость применения которых связана с условиями сооружения и эксплуатации трубопровода.
Местные сопротивления вызывают изменение скорости движения жидкости по значению (сужение и расширение), направлению (колено) или значению и. Направлению одновременно (тройник), поэтому часто указывают на некоторую аналогию между явлениями, наблюдаемыми в местных сопротивлениях, и ударом в твердых телах, который с механической точки зрения также характеризуется внезапным изменением скорости.
На практике местные потери hмп определяют по формуле Вейсбаха
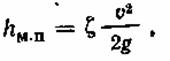
где ζ («дзета») – безразмерный коэффициент, называемый коэффициентом местного сопротивления (значение ζ устанавливают опытным путем); ν – средняя скорость движения жидкости в сечении потока за местным сопротивлением.
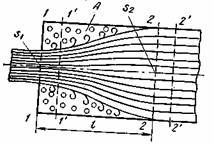
Если по каким-либо соображениям потерю напора желательно выразить через скорость перед местным сопротивлением, необходимо выполнить пересчет коэффициента местного сопротивления. Для этой цели используют соотношение ζ1/ζ2 – (s1/s2)2, где ζ1, ζ2 – коэффициенты местных сопротивлений, соответствующие сечениям s1 и s2.
В некоторых случаях потери напора в местных сопротивлениях удобно определять по так называемой эквивалентной длине – длине прямого участка трубопровода данного диаметра, на которой потеря напора на трение hТР равна (эквивалентна) потере напора hмп, вызы ваемой соответствующим местным сопротивлением. Эквивалентная длина LЭ может быть найдена из равенства потери напора по длине, определяемой по формуле Дарси-Вейсбаха hтр=λ(LЭ/d)[v2/(2g)], и местных потерь напора, учитываемых формулой Вейсбаха hм.п. = ζ[v2/(2g)].
Приравнивая правые части этих формул, находим
LЭ = (ζ/λ)d.
Сложение потерь напора
Во многих случаях при движении жидкостей одновременно наблюдаются потери напора на трение по длине и местные потери напора. В этих случаях полная потеря напора определяется как арифметическая сумма потерь всех видов. Например, полная потеря напора в трубопроводе длиной L, диаметром d, имеющем η местных сопротивлений,

Выражение, стоящее в скобках, называют коэффициентом сопротивления системы и обозначают через ζсист. Таким образом,
![]()
Местные сопротивления можно заменить эквивалентными им длинами. В рассматриваемом случае эквивалентная длина, соответствующая всем η местным сопротивлениям
![]() (*)
(*)
Тогда, обозначая L+LЭ=LП, можно определять сумму потерь по формуле Дарси–Вейсбаха. Для этого в нее вместо действительной длины трубопровода L вводят приведенную длину LП. Таким образом,
![]() (**)
(**)
Формулы (*) и (**) обычно используют при гидравлическом расчете трубопроводов.
Графоаналитические методы расчета трубопроводов
При гидравлическом расчете трубопроводов широко используют графоаналитические методы. Их применение значительно облегчает и упрощает решение некоторых сложных задач, а в отдельных случаях (например, при исследовании совместной работы нескольких центробежных насосов на один общий трубопровод) является единственно возможным приемом, позволяющим получить искомое решение.
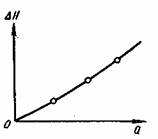
Предположим, что в простейшем случае имеется трубопровод диаметром d и длиной L и по нему перекачивается жидкость, кинематическая вязкость ν которой известна. Потери напора в данном трубопроводе пред ставляют собой функцию только расхода жидкости, т. е. ΔH=f(Q).
Изобразим эту зависимость графически: