Задачи, решаемые в процессе создания систем распознавания

Рефераты >> Психология >> Задачи, решаемые в процессе создания систем распознавания

Отсюда легко определить выражение решающей границы между областями Di, соответствующим классам Wi:

Для двух распознаваемых классов разбиение двумерного пространства выглядит так (рис 2.2). Физически распознавание основывается на сравнении значений той или иной меры близости распознаваемого объекта с каждым классом. При этом если значение выбранной меры близости (сходства) L данного объекта w с каким-либо классом Wg достигает экстремума относительно значений ее по другим классам, то есть

то принимается решение о принадлежности этого объекта классу Wg, то есть wWg.

Надеюсь понятно, что если мера близости не имеет экстремума, то мы находимся на границе, где не можем отдать предпочтение ни одному из классов.

X1 o o o o

xx x o o o

x o o F2(X1,X2) > F1(X1,X2)

x x x o o o o

x o o o o o

x x x x x o o o o o

F1(X1,X2)>F2(X1,X2) x o

x x x x x x x o o

x x x x x x

x x x x x

X2

Рис.2.2

В алгоритмах распознавания, использующих детерминированные признаки в качестве меры близости, используется среднеквадратическое расстояние между данным объектом w и совокупностью объектов (w1,w2, ,wn), представляющих (описывающих) каждый класс. Так для сравнения с классом Wg это выглядит так

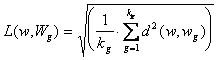
где kg - количество объектов, представляющих Wg-й класс.

При этом в качестве методов измерений расстояния между объектами d(w,wg) могут использоваться любые методы (творческий процесс здесь не ограничивается).

Так, если сравнивать непосредственно координаты (признаки), то

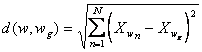
где N - размерность признакового пространства.

Если сравнивать угловые отклонения, то рассматривая вектора, составляющими которых являются признаки распознаваемого объекта w и класса wg, будем иметь:

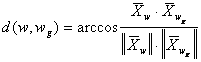
где ||Xw|| и ||Xwg|| - нормы соответствующих векторов.

В алгоритме распознавания, использующем детерминированные признаки можно учитывать и их веса Vj (устанавливать степень доверия или важности). Тогда рассмотренное среднеквадратическое расстояние принимает следующий вид:

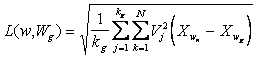
В алгоритмах распознавания, использующих вероятностные признаки, в качестве меры близости используется риск, связанный с решением о принадлежности объекта к классу Wi, где i - номер класса. (i=1,2, ,m.).

Описания классов, как мы недавно рассмотрели

В рассматриваемом случае к исходным данным для расчета меры близости относится платежная матрица вида:

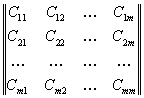
Здесь на главной диагонали - потери при правильных решениях. Обычно принимают Сii=0 или Cii<0.

По обеим сторонам от главной диагонали - потери при ошибочных решениях. В каждой системе эти потери свои, свойственные только ей. Однако назначение их - творчество разработчика системы распознавания.

Если вектор признаков распознаваемого объекта w - , то риск, связанный с принятием решения о принадлежности этого объекта к классу Wg, когда на самом деле он может принадлежать классам W1,W2, .,Wm, наиболее целесообразно определять как среднее значение потерь

С1g, C2g, .,Cmg ,

то есть, потерь, стоящих в g-ом столбце платежной матрицы.

Тогда этот средний риск можно записать как определение МОЖ

Здесь P(Wi/Xw) - апостериорная вероятность того, что wWi.

Для исходных данных, а именно описаний классов эта вероятность легко может быть определена в соответствии с теоремой гипотез или по формуле Байеса

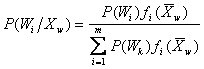
Вероятности и плотности, входящие в формулу - ни что иное как характеристики описания классов в вероятностной системе.

Для алгоритмов, основанных на логических признаках, понятие “мера близости” не имеет смысла. Вспомним упрощенный пример, рассмотренный нами для логических признаков заболеваний (простой простуды и ангины).

Имея значения признаков А,B,C, достаточно подставить их в булевы соотношения между классами и признаками, чтобы сразу получить результат как истинность или ложность булевой функции описания того или иного класса.

Действительно, пусть признаки приняли следующие значения:

-Повышенная температура: A=1

-Насморк: B=0

-Нарывы в горле: C=1

Тогда подстановка их в булевы соотношения даст следующий результат:

То есть, истинным является второе соотношение, соответствующее распознаванию ангины как диагностируемого класса из двух заболеваний.

Для алгоритмов, основанных на структурных (лингвистических) признаках, понятие “меры близости” более специфично.

С учетом того, что каждый класс описывается совокупностью предложений, характеризующих структурные особенности объектов соответствующих классов, распознавание неизвестного объекта осуществляется идентификацией предложения, описывающего этот объект, с одним из предложений в составе описания какого-либо класса.

При этом идентификация может подразумевать наибольшее сходство предложения, описывающего распознаваемый объект с предложениями из наборов описания каждого класса.

Рассмотрев задачу №5 , мы фактически завершили рассмотрение круга задач создания СР. В то же время уже отмечалось, что создание СР осуществляется последовательными приближениями по мере получения дополнительной информации. В этом ряду последовательных приближений главную роль играют признаки распознавания. От эффективности их набора зависит, эффективность системы в целом. В процессе совершенствования системы указанный набор пополняется, неэффективные признаки исключаются. Поэтому одной из задач создания СР должна быть и задача перехода от априорного словаря признаков к рабочему. То же касается и априорного алфавита классов.

ЗАДАЧА № 6

Определение рабочего алфавита классов и рабочего словаря признаков системы распознавания.

Настоящая задача на уровне разработки, прошедшей этапы решения задач 1 - 5, по крайней мере уже может быть поставлена, так как в результате выполнения предшествующих задач создана система распознавания первого приближения (априорный алфавит классов и априорный словарь признаков, выбран алгоритм распознавания).