Рис 2.6.

Если спроецировать вектора и на произвольную ось х, то, учитывая пропорциональность отрезков, отсеченных на сторонах угла параллельными прямыми, можно записать:

.

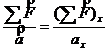Откуда , где - проекция равнодействующей на ось х.

Из рисунка 2.6 также видно, что проекция равнодействующей равно сумме проекций приложенных сил, то есть

,

следовательно, .

Последнее уравнение выражает очень важное следствие: сумма проекций сил, приложенных к телу, по любой оси равна произведению массы тела на проекцию ускорения по этой же оси.

В практике средней школы встречаются физические задачи, которые сводятся к нахождению решений системы уравнений, из которых одни есть уравнения динамики, а другие – кинематики. Если в задаче рассматривается равноускоренное движение, то её решение не зависит от того, проекции или модули векторов входят в уравнения кинематики. Если же в задаче рассматривается равнозамедленное движение, то необходимо предварительно выразить все уравнения системы через однородные величины, то есть через модули соответствующих векторов. В этом случае формула скорости имеет вид , формула пути будет, а формула выразится так .

Несоблюдение этого правила часто приводит к ошибочным решениям. Рассмотрим это на примере следующей задачи (задача №4 из упр. 17 учебника для 9 класса):

«Конькобежец, масса которого равна 50 кг, после разгона скользит по льду, пройдя до остановки 40 м. Сила трения постоянна и равна 10 Н. Сколько времени продолжается торможение?»

рис 2.7

Выполнив чертеж, обращаем внимание учащихся на то, что к конькобежцу приложены три силы: сила тяжести , сила реакции (направленная нормально поверхности движения конькобежца) и сила сопротивления . Рассмотрим проекции этих сил на вертикальную ось y и запишем соответствующее уравнение динамики:

, так как

поскольку , то .

Между тем для проекций на ось х уравнение динамики имеет вид:

откуда (поскольку и ) получим:

, или (где и - модули векторов и ).

Искомую величину - время – можно определить из уравнений кинематики:

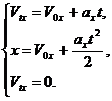
Если теперь выразить проекции векторов через их модули, то получим:

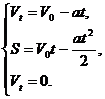
Откуда находим, что , или . Поскольку , то .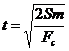

Обычно учащиеся поступают по другому: они записывают уравнения согласно учебнику так:

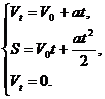
Откуда получают или . Если заранее не сделать разъяснений, то ученики считают, что величины, входящие в формулы, - модули соответствующих векторов и тогда знак минус вызывает у них недоумение. Если же произвести дальнейшее преобразования и подставить в последнюю формулу , то получиться .

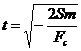Этот результат вызывает у школьников ещё большее неумение, так как им не ясно, как избавиться от знака минус.

В данной задаче легко найти выход из затруднительного положения. Однако в более сложных задачах можно не заметить этого и получить неправильный ответ.

Поэтому имеет смысл на первом этапе решения по динамике рассматривать только случаи равноускоренного движения тел, а затем, после приобретения учащимися прочных знаний навыков, осторожно перейти к анализу и решению задач на равнозамедленное движение.

Глава 3. развитие понятия функции в школьном курсе физике.

§3.1. Функция как важнейшее звено межпредметных связей.

В общей системе теоретических знаний учащихся по физике и математике в средней школе большое место занимает понятие «функция». Оно имеет познавательное и мировоззренческое значение и играет важную роль в реализации межпредметных связей [13].

Функция является одним из основных понятий математики, выражающих зависимость одних переменных величин от других. Как и остальные понятия математики, оно сложилось не сразу, а прошло долгий путь развития, опираясь в начале на представление о переменной величине, а затем на понятия теории множеств.

Трактовка функции как зависимости одних переменных величин от других вводится следующим образом. Если величины x и y связаны так, что каждому значению х соответствует определенное значение y, то y называют функцией аргумента х.

Соотношение между x и y записывают так: . Если связь между х и y такова, что одному и тому же значению х соответствует несколько значений y, то у называют многозначной функцией аргумента х.

Иными словами, это можно сформулировать следующим образом [11], чтобы задать функцию , следует указать: 1) множество значений Х, которое может принимать х (область задания функции); 2) множество значений Y, которое может принимать у (область значения функции); 3) правило, по которому значения х из Х соотносятся со значениями у из Y. В физике чаще всего правило отнесения значениям х соответствующих им значений у задается формулой, устанавливающей, какие вычислительные операции надо произвести над х, чтобы получить у.