Составим уравнение: х - 6 = 4 (х - 18). При решении уравнения у учащихся появляются затруднения, связанные с тем, что возникает необходимость в выполнении дейст­вий с отрицательными числами:

х - 6 = 4х- - 72

х - 4х = - 72 + 6

- 3х = - 66

х = (- 66): (- 3)

х=22

Чтобы избежать таких недоразумений, учитель предлагает на основе изученных свойств числовых равенств (вернее, равно­сильности уравнений) неизвестное перенести в правую часть уравнения:

х- 6=4 (х- 18)

х - 6 = 4х - 72

- 6 = 4х - х - 72

-6 =(4-1) х-72

- 6 = Зх - 72

- 6 + 72 = Зх

72 - 6 = Зх

66=3х

х=22

Как видим, решение уравнения вызывает затруднения у учащихся, и, предвидя это, учи­тель в процессе рассуждения подводит детей к уравнению, решение которого проще:

4 (х- 18)= х-6

4х - 72 = х - 6

4х-х-72=х-х-6

(4- 1) х-72 =-6

Зх = 72 - 6

х = 66 : 3

х = 22 (вагона в первом составе)

Ответ: в первом составе - 22 вагона, во втором - 10.

Обозначив буквой х число вагонов второго состава, в процессе рассуждении можно полу­чить уравнение:

4 (х - 6) = х + 6

4х - 24 = х + 6

Зх = 6 + 24

Зх=30

х= 10

Таким образом, можно с уверенностью ска­зать, что при решении задач алгебраическим способом учителю необходимо продумать, ка­кое неизвестное обозначить буквой, и подвес­ти учащихся к уравнению, решение которого будет проще и понятнее для них.

Выполнение второго задания, предложен­ное автором, для данной задачи сводится к отысканию (узнаванию) среди решенных по­хожей задачи, что отнимает много времени и недостаточно эффективно с точки зрения раз­вития умственных способностей.

Третье задание (составить задачу, похожую на данную) преследует такую же цель, как и второе.

Думается, в данном случае целесообразно решить задачу арифметическим способом. Для осознанного поиска решения задачи необходи­мо проиллюстрировать задачную ситуацию с помощью чертежа. Например, изобразить чис­ло вагонов второго состава отрезком АВ. От состава отцепили 6 вагонов (показываем на чертеже). Оставшееся число вагонов будет со­ответствовать отрезку СВ.

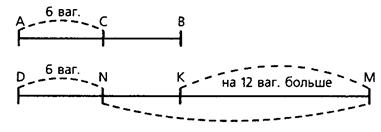В задаче сказано, что вагонов осталось в пер­вом составе в 4 раза больше, чем во втором. Зна­чит, числу оставшихся вагонов первого состава будет соответствовать отрезок в 4 раза больше, чем отрезок СВ (показываем на чертеже отрезок ММ). Первоначально в первом составе было на 6 вагонов больше (показываем на чертеже). DN -отрезок, соответствующий 6 вагонам, тогда ОМ соответствует числу вагонов первого состава).

Рассматривая чертеж, необходимо обра­тить внимание детей на то, что отрезку КМ со­ответствует 12 вагонов. В задаче сказано "на 12 вагонов больше", и эти 12 вагонов прихо­дятся на три равные части, каждая из которых равна отрезку СВ (числу вагонов, оставшихся во втором составе).

После такой наглядной интерпретации за­дачи дети самостоятельно записывают реше­ние и поясняют каждое выполняемое действие:

1)4-1=3 (на 3 части больше осталось ва­гонов в первом составе)

2) 12 : 3 = 4 (вагона осталось во втором составе)

3) 4 + 6 = 10 (вагонов было во втором составе)

4) 10 + 12 = 22 (вагона было в первом составе)

При сравнении способов решения учащие­ся приходят к выводу, что арифметический способ легче и понятнее, чем алгебраический.

Интересным для учащихся будет и реше­ние данной задачи методом перебора.

Прежде всего определим, с какого числа можно (да и нужно) начинать подбор чисел. В задаче сказано, что от каждого состава отцепи­ли по 6 вагонов и при этом вагоны еще оста­лись. Значит, вагонов в составе было больше шести. В задаче также сказано, что в первом составе осталось вагонов в 4 раза больше, чем во втором. Значит, осталось четное число ваго­нов (любое число, умноженное на четное, есть число четное). Если отцепили 6 вагонов (а 6 -число четное), значит, вначале было тоже чет­ное число вагонов (сумма двух четных чисел есть число четное). Во втором составе на 12 вагонов меньше, а это значит, что и во втором составе четное число вагонов. Итак, для пробы будем брать следующие числа: 8, 10, 12 и т.д.

Пусть во втором составе было 8 вагонов, тог­да в первом их было 20 (8 + 12 = 20). Когда от каждого состава отцепили по 6 вагонов, в первом оказалось 14(20-6=14), а во втором-2 (8 - 6 = 2). Проверяем, во сколько раз 14 боль­ше, чем 2(14:2=7)-в7 раз. Это не соответст­вует условию задачи, так как число оставшихся вагонов первого состава должно быть в 4 раза больше, чем число вагонов второго состава. Пусть 10 число вагонов второго состава. Тогда число вагонов первого состава 22 (10 + 12 = 22).

От каждого отцепили по 6 вагонов: во втором ос­талось 4, в первом - 16 (10 - 6 = 4, 22 - 6 = 16). Проверяем, во сколько раз больше осталось ваго­нов в первом составе, чем во втором, и получаем 4(16:4=4), что соответствует условию задачи.

Ответ: в первом составе было 22 вагона, во вто­ром — 10.

Заключение.

Решение текстовых задач и нахождение разных способов их решения на уроках математики способствуют развитию у детей мышления, памяти, внимания, творческого воображения, наблюдательности, последовательности рассуждения и его доказательности; для развития умения кратко, четко и правильно излагать свои мысли.

Решение задач разными способами, получение из нее новых, более сложных задач и их решение в сравнении с решением исходной задачи создает предпосылки для формирования у ученика умения находить свой «оригинальный» способ решения задачи, воспитывает стремление вести «самостоятельно поиск решения новой задачи», той, которая раньше ему не встречалась.

Задачи с многоспособовыми решениями весьма полезны так же для внеклассных занятий, так как при этом открываются возможности по настоящему дифференцировать результаты каждого участника.

Такие задачи могут с успехом использоваться в качестве дополнительных индивидуальных знаний для тех учеников, которые легко и быстро справляются с задачей на уроке, или для желающих в качестве дополнительных домашний заданий.

Список используемой литературы.

1. Бантова М.А. Решение текстовых арифметических задач. Журнал «Начальная школа» №10-11 1989г. МОСКВА. “Просвещение”.

2. Баринова О.В. Дифференцированное обучение решению математических задач. Журнал «Начальная школа» №2 1999г. МОСКВА. “Просвещение”.

3. Вялова С. Как составить и решить задачу. Газета «Начальная школа» №16, №19 1998г. МОСКВА.

4. Гребенникова Н.А. Ознакомление первоклассников с задачей. . Журнал «Начальная школа» №10 1990г. МОСКВА. “Просвещение”.

5. Гребенникова Н.Л. Решение задач на зависимость величин разными способами. Журнал «Начальная школа» №2 1999г. МОСКВА. “Просвещение”.

6. Захарова Н.М. Простые задачи в системе УДЕ. Журнал «Начальная школа» №3 1997г. МОСКВА. “Просвещение”.