Применение метода частотных диаграмм в исследовании устойчивости систем с логическими алгоритмами управления

т.е. подставим сюда вместо коэфициентов а,с, и k их выражения через

, , , тогда получим

-£y(t)= £ (16)

Согласно рис. 5 и условия (16) получаем:

1) при = , y(t)=0

2) при > , y(t)>0

3) при < , y(t)<0,

что и требовалось доказать.

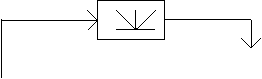
Теперь рассмотрим нашу систему с логическим алгоритмом управления, ее логическая схема приведена на рис. 6.

|x|=c

l g s z

(-) x G(p) (p)

Рисунок 6.

В данном случае считаем что:

- варьируемая величина,

=0.5,

=0.1 (анализ поведения системы при изменении данного параметра исследуется в работе ст-та Новикова, мы берем оптимальное значение),

=0.1,1 (коэффициент обратной связи),

=10,100.

Рассмотрим теперь саму функцию:

W(p)=G(p)W(p),

где G(p) - функция корректора, W(p)= (p)W(p), где

(p)=, а W(p) в свою очередь будет:

W(p)=,

где , соответственно вся функция имеет вид:

W(p)=;

Теперь заменяем p на jw и имеем вид:

;

Для построения гадогрофа выведем формулы для P(w), jQ(w) которые имеют вид:

P(w)=;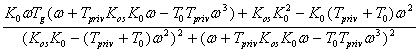

jQ(;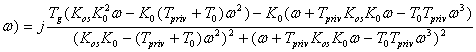

Графики можно посмотреть в приложении N 2.

Учитывая , что добротность x должна быть ³ 0.5¸0.7 мы можем определить добротность нашей системы, она примерно равна 0.5. Отсюдо видно, что из-за увеличения и , x уменьшается, можно сделать вывод, что колебательность звена увеличиться. Это можно наблюдать на графиках 1.13 - 1.16 в приложении N 2.

Страница:

Последние рефераты