Содержание

ВВЕДЕНИЕ

ГЛАВА 1. ЭЙЛЕРОВЫ ЦИКЛЫ

§1. Основные понятия и определения

§2. Критерий существования эйлерова цикла

§3. Алгоритмы построения эйлерова цикла

§4. Некоторые родственные задачи

§5. Задача китайского почтальона

ГЛАВА 2. ГАМИЛЬТОНОВЫ ЦИКЛЫ

§1. Основные понятия и определения

§2. Условия существования гамильтонова цикла

§3. Задачи связанные с поиском гамильтоновых циклов

§4. Методы построения гамильтоновых циклов в графе.

§5. Алгебраический метод построения гамильтоновых циклов

§6. Метод перебора Робертса и Флореса

§8. Улучшение метода Робертса и Флореса

§9. Мультицепной метод

§10. Сравнение методов поиска гамильтоновых циклов

ГЛАВА 3. ЗАДАЧА КОММИВОЯЖЕРА

§1. Общее описание

§2. “Жадный” алгоритм решения ЗК

§3. “Деревянный” алгоритм решения ЗК

§4. Метод лексикографического перебора

§5. Метод ветвей и границ решения ЗК

§6. Применение алгоритма Дейкстры к решению ЗК

§7. Метод выпуклого многоугольника для решения ЗК

§8. Генетические алгоритмы

§9. Применение генетических алгоритмов

СПИСОК ЛИТЕРАТУРЫ

Введение

Целью моей курсовой работы является описание методов нахожде­ния и построения эйлеровых и всех гамильтоновых циклов в графах, а также сравнительный анализ этих методов. Другая цель решаемая в данной работе — это рассмотрение задачи коммивояжера и методов ее решения (включая эвристические и генетические алгоритмы).

Прежде всего, чтобы внести ясность и уточнить терминологию, хотелось бы дать определения некоторым элементам графа таким, как маршрут, цепь, цикл.

Маршрутом в графе G(V,E) называется чередующаяся последова­тельность вершин и ребер: v0,e1, … en,vn, в которой любые два со­седних элемента инцидентны. Если v0 = vn, то маршрут замкнут, иначе открыт.

Если все ребра различны, то маршрут называется цепью. Если все вершины (а значит, ребра) различны, то маршрут называется про­стой цепью.

Замкнутая цепь называется циклом; замкнутая простая цепь на­зывается простым циклом. Граф без циклов называется ациклическим. Для орграфов цепь называется путем, а цикл — контуром.

Глава 1. Эйлеровы циклы

Требуется найти цикл, проходящий по каждой дуге ровно один раз. Эту задачу впервые поставил и решил Леонард Эйлер, чем и за­ложил основы теории графов, а соответствующие циклы теперь называ­ются эйлеровыми. Фигуры, которые требуется обрисовать, не пре­рывая и не повторяя линии, также относятся к эйлеровым циклам.

Задача возникла из предложенной Эйлеру головоломки, получившей название "проблема кенигсбергских мостов". Река Прегель, протекающая через Калининград (прежде город назывался Кенигсбергом), омывает два острова. Берега реки связаны с островами так,

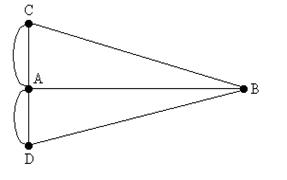В головоломке требовалось найти мар­шрут, проходящий по всем участкам суши таким образом, чтобы каждый из мостов был пройден ровно один раз, а начальный и конечный пункты маршрута совпадали.

§1. Основные понятия и определения

Да­дим теперь строгое определение эйлерову циклу и эйлерову графу. Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называется эйлеровым циклом, а граф называется эйлеровым графом. Если граф имеет цепь (не обязательно простую), содержащую все вершины по одному разу, то такая цепь называется эйлеровой цепью, а граф называется полуэйлеровым графом.

Ясно, что эйлеров цикл содержит не только все ребра по одному разу, но и все вершины графа (возможно, по несколько раз). Оче­видно также, что эйлеровым может быть только связный граф.

Выберем в качестве вершин графа берега реки, а в качестве ребер - мосты, их соединяющие. После этого задача становится оче­видной: требование неосуществимо - чтобы его выполнить, число дуг, приходящих к каждой вершине, должно быть четным. В самом деле, по­скольку по одному мосту нельзя проходить дважды, каждому входу на берег должен соответствовать выход.

§2. Критерий существования эйлерова цикла

Что необходимо, чтобы в графе существовал эйлеров цикл? Во-первых, граф должен быть связанным: для любых двух вершин должен существовать путь, их соединяющий. Во-вторых, для неориентирован­ных графов число ребер в каждой вершине должно быть четным. На са­мом деле этого оказывается достаточно.

Теорема 1. Чтобы в связанном неориентированном графе G существовал эйлеров цикл, необходимо и достаточно, чтобы число вершин нечетной степени было четным.

Доказательство.

Необходимость. Любой эйлеров цикл должен прийти в вершину по одному ребру и покинуть ее по другому, так как любое ребро должно использоваться ровно один раз. Поэтому, если G содержит эйлеров цикл, то степени вершин должны быть четными.

Достаточность. Пусть G — связный неориентированный граф, все вершины которого имеют четную степень. Начнем путь из некоторой произвольной вершины x0 и пойдем по некоторому ранее не использованному ребру к следующей вершине, и так до тех пор, пока не вернемся в вершину x0 и не замкнем цикл. Если все ребра окажутся использованными, то нужный эйлеров цикл построен. Если же некоторые ребра не использованы, то пусть Ф — только что построенный цикл. Так как граф G связен, то цикл Ф должен проходить через некоторую вершину, скажем xi, являющуюся конечной вершиной какого-либо до сих пор не использованного ребра. Если удалить все ребра, принадлежащие Ф, то в оставшемся графе все вершины по-прежнему будут иметь четную степень, так как в цикле Ф должно быть четное число ребер (0 является четным числом), инцидентных каждой вершине.