В качестве еще одного аргумента против использования матрицы смежности приведем теорему о числе шагов, которое

должен выполнить алгоритм, проверяющий на основе матрицы смежности некоторое свойство графа.

Пусть Р — некоторое свойство графа P(G) = 0 или P(G)=1 в зависимости от того, обладает или не обладает G на­шим свойством. Предположим, что свойство Р удовлетворяет следующим трем условиям:

(а) P(G)=P(G'), если графы G и G' изоморфны;

(б) P(G) = 0 для произвольного пустого графа <V,Æ> и P(G)=1 для произвольного полного графа <V, P2(V)> с до­статочно большим числом вершин;

1 2 3 4 5 6 1 2 3 4 5 6

1 0 1 1 0 0 0 1 0 1 1 0 1 0

2 0 0 0 0 0 0 2 1 0 1 0 1 0

3 0 1 0 1 0 0 3 1 1 0 1 0 0

4 0 0 0 0 0 0 4 0 0 1 0 1 1

5 0 0 0 1 0 1 5 1 1 0 1 0 1

6 0 0 0 0 1 0 6 0 0 0 1 1 0

Рис. 2. Матрицы инциденций для графов на рис.1.

(в) добавление ребра не нарушает свойства Р, т. е. P(G)<P(G') для произвольных графов G=(F,E) и G'=(V, E'), таких что Е = Е'.

Примером такого свойства Р является существование цикла (в графе, имеющем, по крайней мере три вершины).

Теорема . Если Р — свойство графа, отвечающее условиям (а), (б), (в), то каждый алгоритм, проверяющий свойство Р (т. е. вычисляющий значение P(G) для данного графа G) на основе матрицы смежности, выполняет в худшем случае Ω(n2) шагов, где n — число вершин графа.

Эта теорема справедлива также для ориентированных гра­фов и для свойств, не зависящих от петель графа, т, е. отве­чающих дополнительному условию

(г) P(G) = P(G') для произвольных ориентированных гра­фов G = < V, E>, G’ = < V, Е> U <v, v>>, v C V.

Более экономным в отношении памяти (особенно в случае, неплотных графов, когда m гораздо меньше n2) является ме­тод представления графа с помощью списка пар, соответствующих его ребрам. Пара <x, у> соответствует дуге <х, у>, если граф ориентированный, и ребру {х, y} в случае неориентиро­ванного графа(рис. 3). Очевидно, что объем памяти в этом случае составляет 2т. Неудобством является большое число шагов — порядка т в худшем случае, — необходимое для по­лучения множества вершин, к которым ведут ребра из данной вершины.

Ситуацию можно значительно улучшить, упорядочив мно­жество пар лексикографически и применяя двоичный поиск, но лучшим решением во многих случаях оказывается структура

Рис.3. Списки ребер соответствующие графам на рис.1.

данных, которую мы будем называть списками инцидентности. Она содержит для каждой вершины v C V список вершин и, таких что v -> u (или v — ив случае неориентированного гра­фа). Точнее, каждый элемент такого списка является записью г, содержащей вершину г. строка и указатель г. след на сле­дующую запись в списке (г. след = nil для последней записи в списке). Начало каждого списка хранится в таблице НАЧАЛО; точнее, HAЧАЛО[v] является указателем на начало спи­ска, содержащего вершины из множества {u: v+u} ({u: v - u} для неориентированного графа). Весь такой список обычно не­формально будем обозначать 3AПИСЬ[v], а цикл, выполняю­щий определенную операцию для каждого элемента и из этого списка в произвольной, но четко установленной последователь­ности, соответствующей очередности элементов в списке, будем записывать «for u C ЗАПИСЬ [v] do .».

Отметим, что для неориентированных графов каждое ребро {u, v} представлено дважды: через вершину v в списке ЗАПИСЬ[u] и через вершину и в списке ЗАПИСЬ[v]. Во многих алгоритмах структура графа динамически модифицируется добавлением и удалением ребер. В таких случаях полагаем, что в наших списках инцидентности элемент списка ЗАПИСЬ [u], содержащий вершину и, снабжен указателем на элемент спи­ска 3AПИCЬ[v], содержащий вершину и, и что каждый эле­мент списка содержит указатель не только к следующему эле­менту, но и к предыдущему. Тогда удаляя некоторый элемент

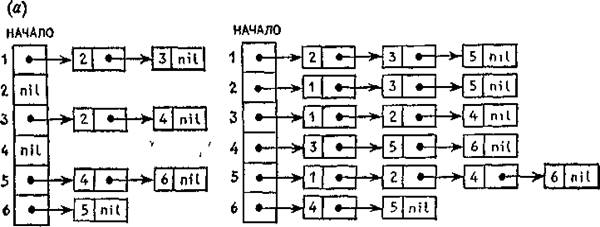
Рис.4. Списки инцидентности ЗПИСЬ[v], v =V, соответствующие графам на рис.1.

из списка, мы можем легко за число шагов, ограниченное кон­стантой, удалить другой элемент, представляющий то же са­мое ребро, не просматривая список, содержащий этот элемент.

Аналогичным способом определяем для каждой вершины и неориентированного графа список ПРЕДШ[v], содержащий вершины из множества (u: u -> v).

Число ячеек памяти, необходимое для представления графа с помощью списков инцидентности, будет, очевидно, иметь по­рядок m + n. На рис.4 представлены списки инцидентности, соответствующие графам на рис. 1.