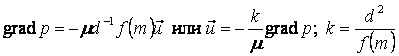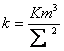1. Физическое описание явления фильтрации жидкости

1.1. Закон фильтрации однородной жидкости

Фильтрация представляет собой движение жидкости в пористой среде под действием перепада давления. Основной характеристикой фильтрационного движения является вектор скорости фильтрации u определяемый следующим образом. Выберем точку М пористой среды и проведем через нее элементарную площадку S. Через выделенную площадку в единицу времени протекает масса жидкости Q. Тогда проекция вектора u на нормаль к выделенной площадке равна lim Δ Q/(p S), где p – плотность жидкости. Подчеркнем, что масса жидкости делится на полную площадь S, а не на ее часть, занятую порами.

Основное соотношение теории фильтрации - закон фильтрации - устанавливает связь между вектором скорости фильтрации и тем полем давления, которое вызывает фильтрационное движение. Некоторые сведения о законе фильтрации можно получить, исходя из самых общих представлений.

Окружим точку пористой среды некоторой малой окрестностью; поле скоростей фильтрации в этой окрестности можно считать непрерывным, а все параметры пористой среды и насыщающей ее жидкости - постоянным. Нельзя пренебречь лишь изменением давления, как бы мало оно не было, поскольку при постоянном по пространству давлении движение полностью отсутствует (по существу это утверждение является основной гипотезой). Поскольку изменение давления в окрестности данной точки определяется градиентом давления, основное предположение при установлении вида закона фильтрации состоит в том, что вектор скорости фильтрации в данной точке пористой среды определяется свойствами жидкости и пористой среды и градиентом давления grad p. Пористая среда характеризуется геометрическими параметрами - характерным размером d и некоторыми безразмерными характеристиками: пористостью m, безразмерными параметрами кривой распределения и др. Закон фильтрации должен являться следствием уравнений количества движения жидкости в поровом пространстве, поэтому в систему определяющих величин следует включить также те характеристики жидкости, которые входят в эти уравнения, т.е. плотность p и вязкостьm. Таким образом, предполагается, что существует зависимость градиента давления grad p от вектора скорости фильтрации u, геометрических характеристик пористой среды m, d и т.д. и характеристик жидкости r и m. Среди величин, от которых зависит grad p, только скорость фильтрации u является вектором. В силу изотропии среды (т.е. независимости ее свойств от вращений и отражений системы отсчета) зависимость grad p от u должна быть инвариантной относительно вращения вокруг направления вектора u.

Поэтому вектор grad p должен быть направлен по одной прямой с вектором u. В самом деле, предположим обратное, т.е. пусть вектор grad p составляет некоторый угол с направлением вектора u. Если повернуть выбранную произвольную систему координат относительно направления вектора u на некоторый угол, то ни вектор u , ни какой-либо другой из определяющих параметров не изменится. Следовательно, не должен измениться и вектор grad p, зависящий только от этих параметров. Но если grad p составляет некоторый угол с направлением вектора u, то при повороте его направление относительно координатных осей обязательно изменится. Отсюда вытекает, что вектор grad p может обращен только по направлению вектора u, так что

grad p= - си, (1)

где с - некоторая скалярная величина, зависящая от модуля вектора скорости u, а также величин d, m, p, m.

Рассмотрим сначала такие фильтрационные движения, для которых несущественны силы инерции. К числу подобных безынерционных движений принадлежит, в силу их крайней медленности, большинство фильтрационных движений, встречающихся на практике. При этом плотность р, характеризующая инерционные свойства жидкости, несущественна и исключается из числа определяющих параметров. Таким образом, при безынерционных движениях величина c зависит только от u, d, m и m. Выпишем размерности интересующих нас величин:

(2)

Из пяти величин (2) можно выбрать три с независимыми размерностями (например, u, m, и d). Тогда, согласно p - теореме, анализа размерностей искомая зависимость будет связывать две безразмерные комбинации указанных величин. В качестве одной из безразмерных величин удобно взять пористость m, в качестве другой выберем cd2/m. Таким образом, имеем

cd2/m= f (m), c=md-2f(m). (3)

После этого уравнение (1) может быть представлено в виде:

(4)

Это соотношение называется законом фильтрации Дарси (по имени французского ученого, установившего его экспериментально в 1856г.). Величина k=d2/f(m), вводимая уравнением (4), носит название проницаемости. Проницаемость имеет разномерность площади; она не зависит от свойств жидкости и является чисто геометрической характеристикой пористой среды.

В физической системе единиц проницаемость измеряется в см2. Однако проницаемость большинства горных пород выражается при этом весьма малыми числами. Так, проницаемость крупнозернистых песчаников составляет 10-8-10-9см2; проницаемость плотных песчаников - около 10-10 см2. Ввиду этого в нефтепромысловой практике получила распространение единица проницаемости 1Д (дарси)= 1,02× 10-8 см2.

В практике гидротехнических расчетов вместо давления обычно используется напор H = p/rg, и закон Дарси записывается в виде:

Величина C, имеющая размерность скорости, называется коэффициентом фильтрации.

Функция f в выражении (3) зависит не только от пористости, но и от других безразмерных характеристик геометрии порового пространства. Были сделаны многочисленные попытки представить в качестве функции пористости и характерного размера для типичных пористых сред как путем рассмотрения простейших моделей, так и путем обработки опытных данных. Все полученные результаты носят частный характер и имеют узкую область применимости. Наибольшей известностью из формул этого рода пользуется уравнение Козени - Кармана, полученное на основе аналогии между пористой средой и системой параллельных трубок, выражающее проницаемость через удельную поверхность å и пористость m: