Пародоксы теории относительности

Рефераты >> Физика >> Пародоксы теории относительности

4. В силу принципа относительности обе системы, "движущаяся" и "неподвижная", абсолютно эквивалентны, и поэтому обратные преобразования от системы кдолжны быть тождественно прямым от к. Обратные преобразования должны отличаться лишь знаком скорости , т.к. системадвижется относительно системывправо со скоростью , а система движется относительно системы (если последнюю считать неподвижной), влево со скоростью . Следовательно, обратные преобразования должны иметь вид 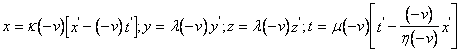. (f) Срав­ни­вая эти преобразования с (e), получаем . Но в силу симметрии получаем, что , т.е. . Очевидно, имеет смысл лишь знак (+), т.к. знак (–) давал бы при перевернутую по и систему. Следовательно . Замечая, что коэффициенты - тоже симметричные функции , первое и последнее уравнение из (e) и (f) можно записать в виде: А) , а) , В) , в) . Умножая А) на , В) на и складывая, получим . 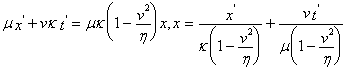Сравнивая это выражение с а), получаем 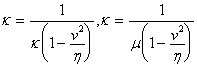. Откуда имеем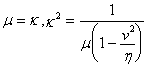

Следовательно, извлекая квадратный корень и замечая, что знак (-) так же, как и для , не имеет смысла, получаем 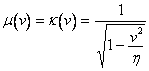. Итак преобразования приобретают вид: 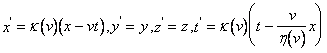(g) или ,подробнее: 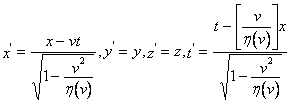,(h) где - неизвестная пока функция .

5. Для определения вида обратимся вновь к принципу относительности. Очевидно, что преобразования (g) должны быть универсальными и применимыми при любых переходах от одних систем к другим. Таким образом, если мы дважды перейдем от системык и от к , то полученные формулы, связывающие координаты и время в системе с координатами и временем в, должны также иметь вид преобразований (g). Это вытекающее из принципа относительности требование, в совокупности с предыдущими требованиями обратимости, симметрии и т.д. означает, что преобразования должны составлять группу.

Воспользуемся этим требованием групповости преобразований. Пусть - скорость системы относительнои - скорость системы относительно системы

Тогда согласно (g)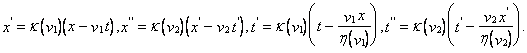

Выражая и через и , получаем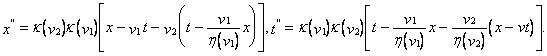

Согласно сформулированному выше требованию эти же преобразования должны записываться в виде (g), т.е. 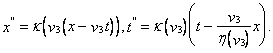(k) Коэффициенты, стоящие при в первой из этих формул и при во второй, одинаковы. Следовательно, в силу тождественности предыдущих формул и этих, должны быть одинаковы и коэффициенты, стоящие при в первой из предыдущих формул и приво второй из формул (h) т.е. 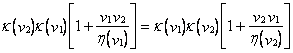. Последнее равенство может быть удовлетворено только при

6. Итак, в преобразованиях (h) h является константой, имеющей размерность квадрата скорости. Величина и даже знак этой константы не могут быть определены без привлечения каких-либо новых допущений, опирающихся на опытные факты.

Если положить , то преобразования (h) превращаются в известные преобразования Галилея Эти преобразования, справедливые в механике малых скоростей (), не могут быть приняты как точные преобразования, справедливые при любых скоростях тел, когда становится заметным изменение массы тел со скоростью. Действительно, учет изменения массы со скоростью приводит к необходимости принять положение об относительности одновременности разобщенных событий. Последнее же несовместимо с преобразованиями Галилея. Таким образом, константа h должна быть выбрана конечной.