Содержание

Введение

Принцип квантования и условия наблюдения квантовых размерных эффектов

Структуры с двумерным электронным газом

Структуры с одномерным электронным газом (квантовые нити)

Структуры с нуль-мерным электронным газом (квантовые точки)

Структуры с вертикальным переносом

Технология квантово-размерных структур

Метод молекулярно-лучевой эпитаксии

Применение квантово-размерных структур в приборах наноэлектроники

Лазеры с квантовыми ямами и точками

Фотоприемники на квантовых ямах

Квантово-точечные клеточные автоматы и беспроводная электронная логика

Использованная литература

Введение

До недавнего времени физики и инженеры электронщики в своих расчетах использовали только законы классической физики. И это было вполне оправдано, т.к., например, электроны в кинескопе движутся так же, как классические материальные точки. Таких примеров можно привести очень много. Однако ситуация меняется. Интегральные схемы становятся все более сложными и объединяют в себе все большее количество элементов, следовательно, должны уменьшаться размеры этих элементов. Эти размеры достигли долей микрона. В этот момент описание на языке классической физики теряет всякий смысл и создатели вынуждены обратиться к квантовой механике.

В классической физике электроны, как и все другие частицы, движутся по траекториям. В любом случае, задав начальную координату и импульс, можно вычислить траекторию.

В квантовой механике картина движения совершенно иная. Эта теория не описывает движение по траектории. Здесь накладывается ограничение на точность, с которой могут быть заданы начальная координата и импульс электрона. Если координата электрона известна с точностью Dx, то его импульс можно определить не точнее, чем Dp ³ h/2pDx. Это соотношение неопределенностей Гейзенберга. Из этого соотношения видно, что очень точное задание координаты электрона приводит к большой неопределенности импульса и, значит, направление, по которому будет двигаться электрон, предвидеть невозможно.

Физики уже накопили большой опыт в разработке приборов, действие которых основано на квантовомеханических принципах. Укладывая атомы с точностью до одного-двух слоев, можно создавать искусственные кристаллы, молекулы и атомы с заданными свойствами. Такие полупроводниковые структуры имеют размеры порядка нескольких нанометров. Можно выделить несколько основных типов микроструктур: квантовые ямы, нити, точки, сверхрешетки. О них в той или иной степени и пойдет речь.

Принцип квантования и условия наблюдения квантовых размерных эффектов

Как должно быть известно читателю, электрон обладает корпускулярно-волновым дуализмом. Следовательно, он может испытывать интерференцию, проникать через узкие щели и барьеры, но вместе с тем сохраняет признаки обычной частицы. Он имеет строго определенную массу и заряд. Кроме того, электрон, подобно классической частице, обладает импульсом и энергией.

Необходимо сказать о главной особенности квантовомеханического описания. Если в некото­рый момент времени частица находилась в ограни­ченной области пространства, то в будущем невоз­можно достоверно предсказать ее местоположение. Можно говорить о распределении частицы в прост­ранстве и о вероятности этого распределения. Ве­личина, описывающая это распределение, получи­ла название Y-функции или волновой функции. Она не описывает ус­редненное поведение большого числа электронов или одного электрона, заряд которого "размазан" по всему пространству, она дает вероятностное, статистическое описание отдельного электрона. Интенсивность этой функции, а точнее, ее квадрат |Y|2 определяет вероятность обнаружить частицу в той или иной области, точнее, вероятность обнару­жить частицу в интервале Dx равна |Y|2Dx. Волновая функция - это основная характеристика квантовой системы. Она содержит полную информацию об электронах или других частицах в атоме, молекуле, кристалле.

Необходимо рассмотреть одно из проявлений чисто квантовой природы электрона. Известно, что волны различной физической природы, возбуждаемые в ограниченном объеме, имеют строго определенную длину волны и частоту. В том случае, когда движение электрона происходит в огра­ниченной области, его энергия имеет строго опре­деленные, дискретные значения. Говорят, что спектр энергий квантован. Если электрон заперт в атоме, мо­лекуле или любой потенциальной яме, то волновая функция Y представляет стоячую волну. Если речь идет о прямоугольной потенциальной яме, которая изображена на рисунке, то по своей форме волна будет такой же, как и в случае 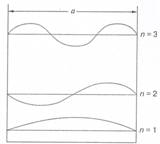натянутой струны, однако, во-первых, природа волны здесь иная, а во-вторых, дискретным в этом случае будет не спектр частот, а спектр энергий. Стоячие волны, описывающие элек­тронные состояния в яме, — это синусоиды, обра­щающиеся в точках x=0 и x=a в нуль. Yn(x) = (Ö(2/a))sin(pxn/a) , где n – номер квантового состояния, a – размер ямы. На данном рисунке изображены три такие функции, соответствующие n = 1, 2, 3, . Видно, что электронная плотность в яме распределяется неравномерно, есть максимумы и минимумы плотности вероятности. Также следует, что длины волн Y-функций, описывающих электронные состояния с различными n, удовлетворяют условиям ln/2 = a/n, то есть в яме укладывается целое число полуволн.

Для наблюдения квантовых размерных эффектов расстояние между энергетическими уровнями должно быть достаточно велико. В первую очередь оно должно значительно превосходить тепловую энергию носителей: En+1 – En >> kT, иначе наблюдение эффектов будет невозможным. Если электронный газ вырожден и характеризуется энергией Ферми V, то желательно также выполнение условия En+1 – En ³ V, при этом первое условие выполняется автоматически, т.к. kT << V; иначе квантовые эффекты имеют весьма малую относительную величину. Существуют и другие условия, связанные с рассеянием носителей на примесях, фононах и др.

Структуры с двумерным электронным газом

Одним из примеров таких структур являются тонкие пленки. В такой структуре одно из направлений (z) очень мало, следовательно, энергетический спектр в этом направлении можно описать формулой En = (hn/a)2/8m, где m – эффективная масса электрона, a – толщина пленки, т.к. в данном направлении образуется потенциальная яма. В оставшихся двух направлениях электроны могу передвигаться свободно. Образованную потенциальную яму надо считать бесконечно глубокой, следовательно, En должны быть малы по сравнению с действительной глубиной ямы Ф. Данное условие приводит к толщине пленки порядка нанометров, что соответствует нескольким межатомным расстояниям. Полная энергия носителей в квантово-размерной пленке носит смешанный дискретно-непрерывный спектр: E = En +(px2 + py2)/2m, где px и py – компоненты импульса в плоскости слоя.