Основы специальной теории относительности и релятивистская механика

Рефераты >> Физика >> Основы специальной теории относительности и релятивистская механика

Обозначим через - скорость световой волны в неподвижном эфире и через - скорость световой волны в неподвижной призме. Тогда, согласно волновой теории света, показатель преломления стекла призмы равен

Согласно гипотезе Френеля о частичном увлечении эфира, скорость света в движущейся призме равна

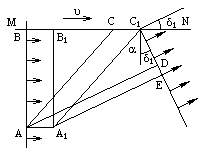
Найдем значение угла , на который отклоняется фронт (или луч) света от звезды, проходя через движущуюся призму .

Рассматривая прямоугольные и с общей гипотенузой , для отрезков и получаем очевидные соотношения:Таким образом,

Вычислим теперь отрезки и по-другому. Очевидно из рисунка, что имеем следующие простые соотношения:Из приведённого чертежа имеем, кроме того, также следующие соотношения: где - угол поворота фронта волны после прохождения его через призму. Таким образом,Учтём теперь, чтои что при малых имеем приближённое равенствопри этом, считая отношение малым, мы заменили угол , на угол , его значение при . Учтём, кроме того, что при малой разности имеем приближённое равенство

Приходим, таким образом, к следующему приближённому уравнению для определения угла :При и очевидно отсюда имеем соотношениесправедливое для неподвижной призмы, которое позволяет сократить в вышеприведённом уравнении члены нулевого порядка в обеих частях приведённого равенства. Тогда окончательно придём к уравнениюПреобразуем выражение, стоящее в правой части. Очевидно, чтоТаким образом, приходим к уравнениюкоторое позволяет вычислить угол отклонения луча от звезды, движущейся со скоростью , призмой, если известен угол отклонения для этого луча покоящейся призмой.

В качестве луча, отклонение которого мы рассмотрим, возьмём луч , изображённый на рисунке. Как видим, угол преломления в движущейся призме всегда несколько меньше угла преломления в покоящейся призме.

Проследим теперь за дальнейшей судьбой луча после выхода его из призмы. Этот луч света, вышедший из призмы, движущейся вместе с Землёй, из-за движения Земли, попадёт на экране, тоже движущемся, как и призма, со скоростью , не в точку , а в точку , которая определяется из условия, что за время, пока свет распространится от точки до точки , двигаясь со скоростью , точка попадёт в точку , двигаясь со скоростью .

Таким образом, если -время распространения света от точки до точки , то

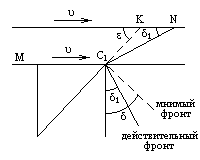
Рассмотрим теперь косоугольный C1KN и применим к нему теорему синусов. Получим соотношение:

следовательно:

Учитывая, что , получаем: