Классификация систем массового обслуживания и их основные элемент

Рефераты >> Экономическая теория >> Классификация систем массового обслуживания и их основные элемент

Сформулируем, в чем заключается особенность изучаемых нами задач в сделанных предположениях. Пусть в некоторый момент наша система находилась и состоянии . Докажем, что последующее течение процесса обслуживания не зависит в смысле теории вероятностей от того, что происходило до момен­та . Действительно, дальнейшее течение обслуживания пол­ностью определяется тремя следующими факторами:

моментами окончания обслуживаний, производящихся в мо­мент ;

моментами появления новых требований;

длительностью обслуживания требований, поступивших после .

В силу особенностей показательного распределения длитель­ность остающейся части обслуживания не зависит от того, как долго уже продолжалось обслуживание до момента . Так как поток требований простейший, то прошлое не влияет на то, как много требований появится после момента . Наконец длительность обслуживания требований, появившихся после , никак не зависит от того, что и как обслуживалось до момента .

Известно, что случайные процессы, для которых будущее развитие зависит только от достигнутого в данный момент состояния и не зависит от того, как происходило развитие в прошлом, называются процессами Маркова или же процессами без последействия. Итак, система с ожиданием в случае простейшего потока и показательного времени обслуживания представляет собой случайный процесс Маркова. Это обстоятельство об­легчает дальнейшие рассуждении.

3. Составление уравнений.

Задача теперь состоит в том, чтобы найти те уравнения, которым удовлетворяют вероятности . Одно из уравнения очевидно, a именно для каждого t

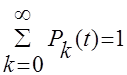(2)

Найдём сначала вероятность того, что и момент t.+h все приборы свободны. Это может произойти следующими способами:

· в момент t все приборы были свободны и за время h новых требований не поступало;

· в момент t один прибор был занят обслуживанием требования, все остальные приборы свободны; за время h обслуживание требования было завершено и новых требований не поступило.

Остальные возможности, как-то: были заняты два или три прибора и за время h работа на них біла закончена - имеют вероятность о(h), как легко в этом убедится.

Вероятность первого из указанных событий равна

,

вероятность второго события

.

Таким образом

.

Отсюда очевидным образом приходим уравнению

Перейдём теперь к составлению уравнений для при 1. Рассмотрим отдельно два различных случая: 1и . Пусть в начале 1. Перечислим только существенные состояния, из которых можно прийти в состояние в момент t+h. Эти состояния таковы:

В момент t система находилась в состоянии , за время h новых требований не поступило и ни один прибор не окончил обслуживания. Вероятность этого события равна:

В момент t система находилась в состоянии , за время h поступило новое требование, но ни одно ранее находившееся требование не было закончено обслуживанием. Вероятность этого события равна

В момент t система находилась в состоянии , за время h новых требований не поступило, но одно требование было обслужено. Вероятность этого равна

Все остальные мыслимые возможности перехода в состояние за промежуток времени h имеют вероятность, равную о(h).

Собрав воедино найденные вероятности, получаем следующее равенство:

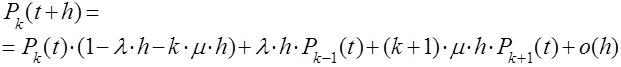Несложные преобразования приводят от этого равенства к такому уравнению для 1;

(4)

Подобные же рассуждения для приводят к уравнению

(5)

Для определения вероятностей получили бесконечную систему дифференциальных уравнений (2)-(5). Её реше­ние представляет несомненные технические трудности.

4. Определение стационарного решения.

В теории массового обслуживания обычно изучают лишь установившееся решение для . Существование таких решений устанавливается так называемыми эргодическими теоремами, некоторые из них позд­нее будут установлены. В рассматриваемой задаче оказывается, что предельные или, как говорят обычно, стационарные вероятности существуют. Введём для них обозначения . За­метим дополнительно, что при .

Сказанное позволяет заключить, что уравнения (3), (4), (5) для стационарных вероятностей принимают следующий вид:

(6)

при 1

(7)

при

(8)