Линеаризованная система имеет вид:

(15)

Приняв во внимание, что в длинном нефтепроводе у нас будут отсутствовать инерционные силы, первое слагаемое во втором уравнении можно принять равным нулю.

Система уравнений примет вид:

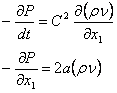(16)

Перейдем к реальным параметрам трубопровода. – массовый расход.

Получим:

(17)

Примем а .

(18)

Система дифференциальных уравнений (18) является математической моделью линейного нефтепровода.

Статический режим работы линейного нефтепровода.

Для рассмотрения статического режима линейного нефтепровода воспользуемся вторым уравнением системы (18)

где .

Т.к. получим.

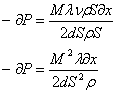
Приняв во внимание то, что получим.

Проинтегрировав это уравнение

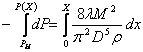
получим:

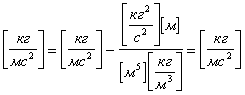
Коэффициент гидравлического сопротивления определяется по формуле А. Д. Альтшуля.

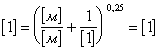
Число Рейнольдса определяется по формуле где – вязкость. Число Рейнольдса безразмерная величина.

Проверим.

Вычислим число Рейнольдса:

.

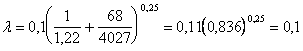
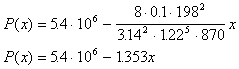
Построим график статического режима линейного трубопровода.

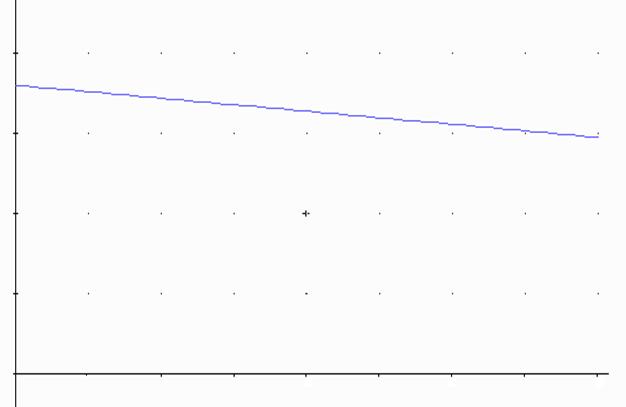
Динамический режим работы линейного нефтепровода.

Допустим, что у нас был установившийся режим, характеризующийся при:

.

Пусть в какой-то момент времени t = 0 на входе Р

был создан скачек: , но давление на

выходе нефтепровода не изменилось. Нас будет ин-

тересовать как изменится давление в любой точке t

нефтепровода.

Воспользуемся ранее выведенной системой дифференциальных уравнений (18).

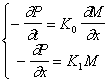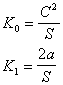где (1)

Дифференцируя второе уравнение по х и учитывая первое, получим уравнение:

. (2)

Для упрощения уравнения примем , тогда уравнение запишем:

. (3)

Напишем для него начальные и граничные условия:

Начальные условия: .

при:

где есть единичный скачек.

Решим уравнение (3) используя метод преобразования Лапласа.

Для этого, вместо Р введем вспомогательную величину Р*, такую что

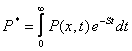где S - оператор (4)

тогда граничные условия перепишутся в виде:

1.

2. 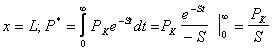(5)

Умножим обе части уравнения (3) на e-St и проинтегрируем в пределах от 0 до во времени

(6)

Рассмотрим левую часть уравнения

. (7)

Рассмотрим левую часть уравнения

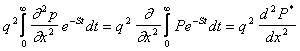. (8)

Приравниваем обе части:

. (9)

Найдем сначала решение однородного уравнения

. (10)

Пусть Р* определяется как .

Нам необходимо определить и С

откуда , а .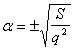

Тогда решением уравнения является

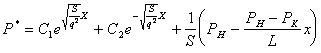(11).

Для определения коэффициентов С1 и С2 учтем граничные условия

х=0; 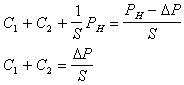(12)

x = L; (13)

отсюда выразим значения С1 и С2 : ,

(14).

Подставив найденное значение коэффициентов в (11) окончательно получаем:

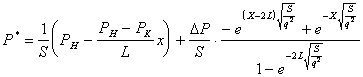(15).

Применим к выражению (15) обратное преобразование Лапласа

(16)