После несложных преобрахований получаем дифференциальные уравнения для формирующих фильтров двух входов.

Третьей фазовой координатой будет x, значение на входе в третью нелинейность. Его уравнение имеет вид:

Эти уравнения и составят систему дифференциальных уравнений:

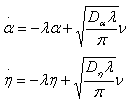2 Расчет системы в нелинейной форме

Для расчета данной системы в нелинейном виде была разработана соответствующая программа которая интегрировала систему уравнения методом Рунге-Кутта четвертого порядка.

Для решение дифференциального уравнения методом Рунге-Кутта необходимо знать начальные условия, то есть значения вектора состояний в нулевой момент времени, в данном случае они нулевые.

После осуществления интегрирования результаты были записаны в файл, и затем построены. Графики имеют следующий вид:

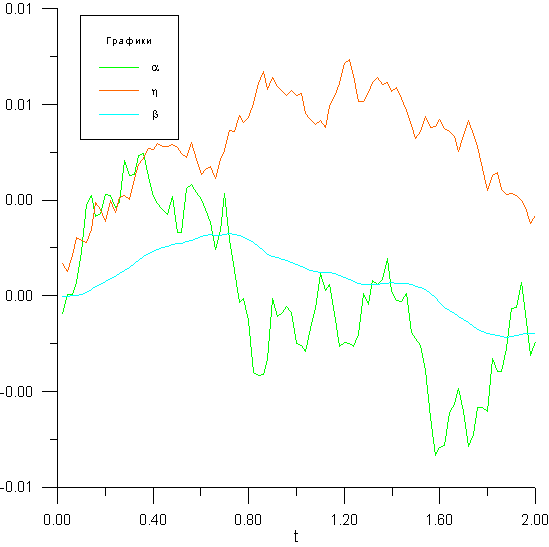Рисунок 1.

3 Расчет линеаризованной системы

Для расчета системы в линеаризованным виде по формулам, необходимо линеаризовать систему дифференциальных уравнений, т. е. заменить три нелинейных элемента линейными как это показано в 2.5. Для того чтобы получить коэффициенты статистической линеаризации нам необходимо знать параметры случайного процесса на входе в нелинейность (математическое ожидание и дисперсию). Параметр входа в третью нелинейность имеется в векторе состояний. Поэтому его дисперсия присутствует в матрице ковариации. Для нахождения дисперсий на входе в первую и вторую нелинейности произведем следующие действия. Преобразуем систему таким образом чтобы входом системы оставался один из входов в нашу систему, а выходом вход в нелинейность (два входа рассматриваются отдельно, а затем их дисперсии складываются).

Итак, посчитаем дисперсии от воздействий a и h, на входах первой и второй нелинейности:

Назовем сигнал на входе в первую нелинейность х, во вторую y тогда уравнение связывающие x и a будут иметь вид:

Здесь коэффициенты статистической линеаризации соответственно первой и второй нелинейностей, далее:

Следовательно передаточная функция будет иметь вид:

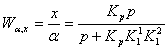
Спектральная плотность случайного процесса на входе a имеет вид:

Тогда дисперсия на входе первой нелинейности будет иметь вид:

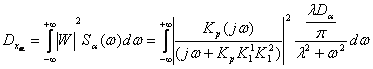
В теории известно, что интегралы вида:

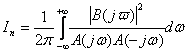
где:

В аналитической форме имеют вид:

, где

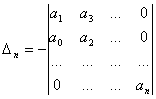
Рассмотрим отдельно знаменатель нашего интеграла, приведенный к виду:

Тогда:

Отсюда следует:

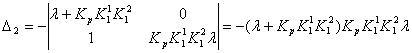
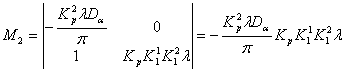
Откуда:

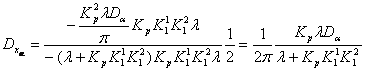
Рассуждая аналогичным образом получим остальные дисперсии:

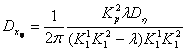
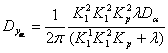
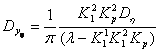
Отсюда следует, что дисперсия на входе в первую нелинейность имеет вид:

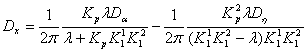
На входе второй нелинейности:

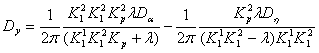
Далее необходимо получить выражения для самих коэффициентов статистической линеаризации, воспользовавшись выведенными раньше соотношениями. Легко видеть, что все интегралы в этих формулах будут иметь один из трех, ниже перечисленных, видов:

Эти интегралы, считаются в численном виде и получаются с помощью функции ошибок и гауссовской плотности вероятности. Они реализованы в программе в виде функций, тогда коэффициенты статистической линеаризации для первого нелинейного элемента будут иметь вид:

K0=k2*J1(0,-s,m,D,-1)+l1*J0(0,-s,m,D,-1)+

k1*J1(-s,s,m,D,0)+k2*J1(s,0,m,D,1)+l2*J0(s,0,m,D,1);

K1=(k2*J2(0,-s,m,D,-1)+l1*J1(0,-s,m,D,-1)+k1*J1(-s,s,m,D,0)+

k2*J2(s,0,m,D,1)+l2*J1(s,0,m,D,1)-m*K0)/D;

Для второго:

K0=-s*J0(0,-s,m,D,-1)+J1(-s,s,m,D,0)+s*J0(s,0,m,D,1);

K1=(-s*J1(0,-s,m,D,-1)+J2(-s,s,m,D,0)+s*J1(s,0,m,D,1)+

s*m*J0(0,-s,m,D,-1)-m*J1(-s,s,m,D,0)-s*m*J0(s,0,m,D,1))/D;

Для третьего:

K0=-s*J0(0,-s,m,D,-1)+J1(-s,s,m,D,0)+s*J0(s,0,m,D,1);

K1=(-s*J1(0,-s,m,D,-1)+J2(-s,s,m,D,0)+s*J1(s,0,m,D,1)+

s*m*J0(0,-s,m,D,-1)-m*J1(-s,s,m,D,0)-s*m*J0(s,0,m,D,1))/D;

Линеаризованная система должна иметь вид: