Сравнительный анализ рециркуляционных схем на примере реакции изомеризации

Рефераты >> Химия >> Сравнительный анализ рециркуляционных схем на примере реакции изомеризации

Таблица 2.1. Численная зависимость величины рецикла от суммарного объема реакторов при подаче рецикла на вход первого реактора.

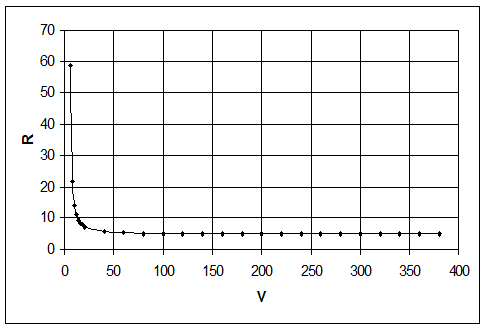Рис.2.2. Зависимость величины рецикла от суммарного объема реакторов при подаче рецикла на вход первого реактора.

Из графика видно, что с увеличением рецикла объем уменьшается и наоборот.

Поэтому для проведения какого-либо процесса следует выбирать оптимальное соотношение объема и величины рецикла.

2.2. Рециркуляционная схема с рециклом, охватывающим один реактор.

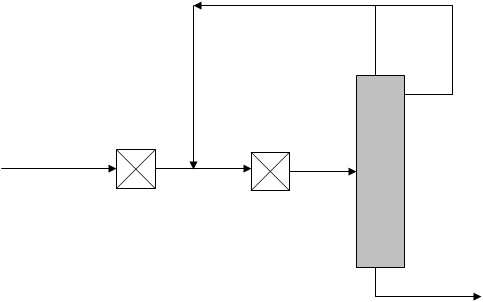
Рассмотрим рециркуляционную систему (рис.2.2), состоящую из двух реакторов идеального смешения и ректификационной колонны, где рецикл охватывает только один реактор.

В реакторах протекают обратимые реакции типа AB, скорость которых подчиняется закону действующих масс. На вход в систему подается чистый реагент А, реакционная смесь зеотропна, колонна обладает бесконечной эффективностью по разделению, реагент А является легколетучим компонентом. Тогда в соответствии с обозначениями на (рис.2.3) система балансовых уравнений в статике относительно реагента А имеет вид:

Для смесителя:

G = F + R (2.25)

Gxg = Fxf1 + Rxr (2.26)

R Xr

V1 V2

F F G L

Xf Xf1 Xg Xl2

W, Xw

Рис.2.3. Рециркуляционная система. Реактор-ректификационная колонна.

С охватом рециклом одного реактора.

Для колонны:

L = W + R (2.27)

Lxl2 = Wxw + Rxr (2.28)

Для реакторов:

Для первого реактора:

Fxf = Fxf1 + V1rA1 (2.29)

Где rA1 = k+xf1 – k-(1 – xf1) (2.30)

Для второго реактора:

G = F + R (2.31)

Fxf1 + Rxr = Lxl2 – V2rA2 (2.32)

Где rA2 = k+xl2 – k-(1 – xl2) (2.33)

Для системы в целом:

Fxf – Wxw = rA1V1 + rA2V2 (2.34)

Где rA1, rA2 – скорости химической реакции по реагенту А в первом и втором реакторах, V1, V2 – объемы реакционной зоны.

Выразим скорость химической реакции, протекающей в первом реакторе.

Для этого из (2.30) выразим сдержание компонента А на выходе из реактора xf1

Xf1 = (2.35)

И подставим его в выражение (2.29), принимая, что на вход в систему подается чистый компонент А, xf = 1:

F – – V1rA1 = 0 (2.36)

После преобразований:

rA1 = (2.37)

Теперь выразим скорость химической реакции, протекающей во втором реакторе:

Содержание компонента А на выходе из реактора

xl2 = (2.38)

Подставим (2.38) и (2.35) в (2.32), принимая, что в рецикле чистый компонент А, xr = 1:

(2.39)

После преобразований

rA2 = (2.40)

затем, подставляя (2.37), получим выражение для скорости химической реакции во втором реакторе:

rA2 = (2.41)

Для того чтобы достичь полного превращения сырья производительность реактора должна равняться количеству реагента А, поступающего на вход в систему

F = rA1V1 + rA2V2 (2.42)

Подставим выражения (2.37) и (2.41) в (2.42):

F = (2.43)

После преобразований

L = (2.44)

где L = R + F.

Мы получили аналитическую зависимость величины рецикла от объема реакторов.

По этому выражению мы можем построить и проследить зависимость величины рецикла от объема реакторов.

Примем k+, k - и F постоянными, а объемы реакторов равными между собой

V1 = V2.

k+ = 2

k - = 1

F = 10кмоль/час. При этих значениях с помощью программы Eсxel численно просчитаем, по формуле (2.44), зависимость величины рецикла от объема. Результаты представлены в таблице 2.2.

Продолжение.