Теория растворов
Используя закон распределения, можно рассчитать процесс экстрагирования. Пусть вещество подлежащее извлечению находится в растворе объёмом V в количестве, и пусть для извлечения его из раствора используют подходящий растворитель объёмом. Если к раствору объёмом V добавить растворитель 
и смесь хорошо перемешать до наступления равновесия, то часть растворённого вещества из раствора перейдёт в растворитель. Обозначим количество извлечённого вещества оставшегося в растворе, тогда его концентрация в этом растворе 
. Его концентрация в 
. Коэффициент распределения 
. 
Количество извлечённого вещества 
. Если отделить раствор с помощью делительной воронки, к оставшемуся раствору в котором извлечённого вещества добавить свежеприготовленного растворителя , то обозначим через количество растворённого вещества в растворе после второго экстрагирования. Будем иметь 
;
; 
. Если экстрагировать n- раз 
, где 
- количество извлекаемого вещества которое осталось в растворе V n-го после экстрагирования. Количество извлечённого вещества при этом определяется 
. если экстрагировать 1 раз, но V 
, то количество экстрагированного вещества определяется 
. Эффективнее экстрагировать 
раз обьёмом V чем один раз - .
Совершенные растворы
Образуются в том случае, если компоненты весьма близки по своим физикохим. свойствам (растворы оптических изомеров, расплавы близких по свойствам природных веществ (Fe и Ni). Совершенные растворы, образованные без изменения V и без теплового эффекта. По этой причине V и Н бинарного совершенного раствора выражается уравнением: 
, здесь и - молярный V 1-ого и 2-ого компонентов, а и - молярные энтальпии этих компонентов в чистом виде 
; 
. Парциальный молярный V равен просто молярному V 
; 
т.к. 
то 
, это означает, что тенденция к образованию такого раствора определяется увеличением энтропии 
. В отличии от величин Н и V величины G и S преобр. совершенного раствора не аддитивны. Энтропия S определяется отношением: 
; 
- энтропии чистых компонентов относящихся к 1 молю, а – изменение энтропии при смешении компонентов. Изменение энтропии при смешении 1 и 2 компонента определяется: 
. Изменение энтропии при образовании 1 моля раствора 
. Изменение G при образовании 1 моля раствора 
. Т к 
и 
, то 
, то есть совершенный раствор образуется самопроизвольно при любых концентрациях, при любых соотношениях компонентов. Для любого компонента совершенного раствора хим. потенциал определяется 
: . Для обоих компонентов бинарного совершенного раствора при любых его концентрациях соблюдается закон Рауля 
и 
. Давление пара над раствором 
; 
. Как парциальное давление каждого компонента так и общее давление пара над раствором является линейной функцией состава.
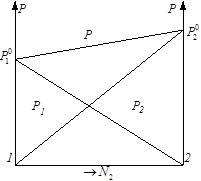
Чтобы построить диаграмму давление-состав для совершенного раствора, достаточно знать лишь давление насыщенного пара каждого из компонентов в чистом состоянии при данной температуре. В случае совершенного раствора легко определить состав пара над раствором. В общем случае составы равновесных жидкости и пара не совпадают. Обозначим и – молярные доли 1 и 2 компонента в насыщенном паре над раствором. По закону Рауля и . По закону Дальтона 
и 
, где –P общее давление пара над раствором 
а 
. и 
Соответственно 
по этим формулам можно подсчитать молярные доли компонентов в равновесной паре над совершенным раствором, если известен состав раствора. Сопоставив закон Рауля и Дальтона можно написать 
. Составы пара и жидкости будут одинаковы только тогда, когда будут равны давлению насыщенного пара компонентов в чистом состоянии, что бывает очень редко. Если 
, то есть компонент первый при данной температуре более летуч, то пар будет обогащен по сравнению с жидкостью именно этим компонентом, то есть 
. В случае совершенных растворов пар всегда обогащен по сравнению с жидкостью компонентом, давление насыщенного пара которого выше, то есть более летучим компонентом.
