Заметим, что при оценке вероятности мы использовали только два корня многочлена f(x). При n > 2 эта вероятность, конечно, ещё меньше. Более тонкий анализ с использованием оценок А. Вейля для сумм характеров показывает, что вероятность для многочлена f(x) не распасться на множители при однократном проходе шагов алгоритма 1-4 не превосходит 2-n + O(p-1/2). Здесь постоянная в O(.) зависит от n. В настоящее время известно элементарное доказательство оценки А. Вейля.

Если в сравнении (1) заменить простой модуль p составным модулем m, то задача нахождения решений соответствующего сравнения становится намного более сложной. Известные алгоритмы её решения основаны на сведении сравнения к совокупности сравнений (1) по простым модулям – делителям m, и, следовательно, они требуют разложения числа m на простые сомножители, что, как уже указывалось, является достаточно трудоёмкой задачей.

3.2 Произведение и возведение в степень многочленов, заданных массивами

Условимся представлять многочлены массивами, индексированными, начиная с 0, в которых элемент с индексом i означает коэффициент многочлена степени i

type

Polynome=array[1 Nmax] of Ring_Element;

Следующий алгоритм даёт функцию умножения двух многочленов и , где многочлен степени (который даёт результат в конце алгоритма) должен быть предварительно инициализирован нулём.

for i:= 0 to degP do

for j:= 0 to degQ do

R[i+j]:=R[i+j]+P[i]*Q[i];

Изучая предыдущий алгоритм, устанавливаем, что его сложность как по числу перемножений, так и сложений, равна произведению высот двух многочленов: (deg P + 1)(degQ + 1), но в этом алгоритме, который не учитывает случай нулевых коэффициентов, можно рассматривать высоту многочлена как число всех коэффициентов. Значит, возможно улучшить предыдущий алгоритм, исключив все ненужные перемножения:

for i:= 0 to degP do

if P[i] ¹ 0 then

for j:= 0 to degQ do

if Q[j] ¹ 0 then

R[i+j]:=R[i+j]+P[i]Q[i];

Очень просто вычислить сложность алгоритма возведения в степень последовательными умножениями, если заметить, что когда P – многочлен степени d, то Pi – многочлен степени id. Если обозначить Cmul(n) сложность вычисления Pn, то рекуррентное соотношение Cmul(i + 1) = Cmul(i) + (d +1)(id +1) даёт нам:

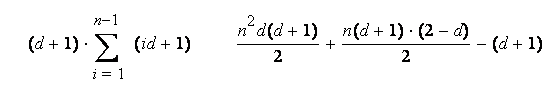Cmul(n) = =

Что касается возведения в степень с помощью дихотомии (т.е. повторяющимися возведениями в квадрат), вычисления несколько сложнее: зная , вычисляем с мультипликативной сложностью. Как следствие имеем:

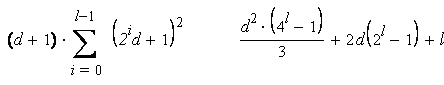Csqr(2l) = = =

=

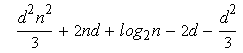Предварительное заключение, которое можно вывести из предыдущих вычислений, складывается в пользу дихотомического возведения в степень: если n есть степень двойки (гипотеза ad hoc), этот алгоритм ещё выдерживает конкуренцию, даже если эта победа гораздо скромнее в данном контексте (n2d2/3 против n2d2/2), чем когда работаем в Z/pZ (2log2 n против n).

Но мы не учли корректирующие перемножения, которые должны быть выполнены, когда показатель не является степенью двойки. Если n = 2l+1 – 1, нужно добавить к последовательным возведениям в квадрат перемножения всех полученных многочленов. Умножение многочлена степени (2i-1)d на многочлен степени 2id вносит свой вклад из ((2i – 1)d + 1)( 2i d + 1) умножений, которые, будучи собранными по всем корректирующим вычислениям, дают дополнительную сложность:

= =

=

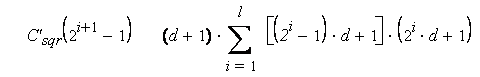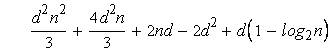
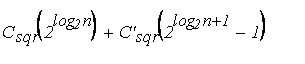
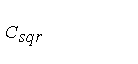
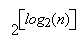Теперь можно заключить, что дихотомическое возведение в степень не всегда является лучшим способом для вычисления степени многочлена с помощью перемножений многочленов. Число перемножений базисного кольца, которые необходимы, Csqr(n), - в действительности заключено между ( ) и т.е. между n2d2/3 и 2n2d2/3, тогда как простой алгоритм требует всегда n2d2/2 перемножений. В частности, если исходный многочлен имеет степень, большую или равную 4, возведение в степень наивным методом требует меньше перемножений в базисном кольце, чем бинарное возведение в степень, когда n имеет форму 2l – 1.

Можно довольно просто доказать, что если n имеет вид 2l +2l – 1 + c (выражения, представляющие двоичное разложение n), то метод вычисления последовательными перемножениями лучше метода, использующего возведение в квадрат (этот последний метод требует корректирующего счёта ценой, по крайней мере, n2d2/9). Всё это доказывает, что наивный способ является лучшим для этого класса алгоритмов, по крайней мере, в половине случаев.

Действительно, МакКарти [3] доказал, что дихотомический алгоритм возведения в степень оптимален среди алгоритмов, оперирующих повторными умножениями, если действуют с плотными многочленами (антоним к разреженным) по модулю m, или с целыми и при условии оптимизации возведения в квадрат для сокращения его сложности наполовину (в этом случае сложность действительно падает приблизительно до n2d2/6 + n2d2/3 = n2d2/2).

3.3 Небольшие оптимизации для произведений многочленов

В принципе вычисление произведения двух многочленов степеней n и m соответственно требует (n +1)( m +1) элементарных перемножений. Алгоритм оптимизации возведения в квадрат состоит просто в применении формулы квадрата суммы:

что даёт n +1 умножений для первого члена и n( n +1)/2 – для второго, или в целом (n +1)( n +2)/2 умножений, что близко к половине предусмотренных умножений, когда n большое.