Вычисление определённых интегралов по правилу прямоугольников

[0 ,h] такие, что

В силу доказанного замечания на сегменте [-h, h] найдётся точка такая, что

Поэтому для полусуммы мы получим следующее выражение:

Подставляя это выражение в равенство (3), получим, что

(4)

где

. (5)

Так как величина представляет собой площадь некоторого прямоугольника с основанием (рис.1), то формулы (4) и (5) доказывают, что ошибка, совершаемая при замене 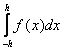указанной площадью, имеет порядок

Таким образом, формула тем точнее, чем меньше h. Поэтому для вычисления интеграла естественно представить это интеграл в виде суммы достаточно большого числа n интегралов

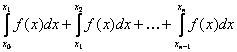
И к каждому из указанных интегралов применить формулу (4). Учитывая при этом, что длина сегмента равна , мы получим формулу прямоугольников (1), в которой

Здесь . Мы воспользовались формулой, доказанной в утверждении, для функции

Примеры вычисления определённых интегралов

по формуле прямоугольников.

Для примеров возьмём интегралы, которые вычислим сначала по формуле Ньютона-Лейбница, а затем по формуле прямоугольников.

П р и м е р 1. Пусть требуется вычислить интеграл .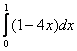

По формуле Ньютона-Лейбница, получим

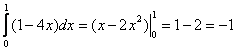
Теперь применим формулу прямоугольников

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

Сумма .

Таким образом, .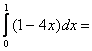

В данном примере неточности в вычислениях нет. А значит, для данной функции формула прямоугольников позволила точно вычислить определённый интеграл.

П р и м е р 2. Вычислим интеграл с точностью до 0,001.

Применяя формулу Ньютона-Лейбница, получим .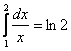

Теперь воспользуемся формулой прямоугольников.

Так как для имеем (если ), то

Если взять n=10, то дополнительный член нашей формулы будет Нам придётся внести ещё погрешность, округляя значения функции; постараемся, чтобы границы этой новой погрешности разнились меньше чем на С этой целью достаточно вычислять значение функции с четырьмя знаками, с точностью до 0,00005. Имеем: