III. Малые возмущения системы линейных уравнений

В этой задаче рассматривается система:

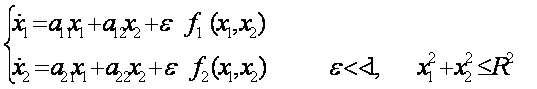
с действительными коэффициентами аij.

Необходимо исследовать фазовые кривые этой системы:

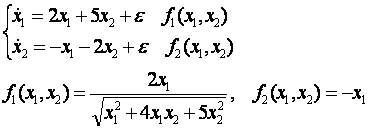
(1)

Сведем систему (1) к системе вида:

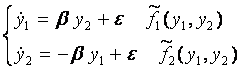
(2)

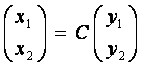
с помощью замены

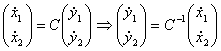
(3)

Запишем систему (1) в виде

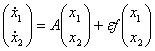, где (4)

Подставим в систему (4), а в систему (3), тогда получим:

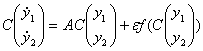
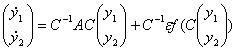
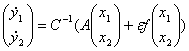
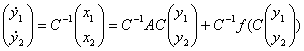(5)

Найдем собственные значения матрицы А:

,

Систему (2) можно записать в виде:

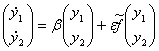, где (6)

Из системы (5) и (6) следует, что

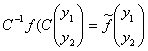
Подберем матрицу С такую, что пусть и AC = CB

=

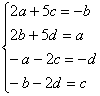
Решив эту систему, получим: a=-2, b=-1, c=1, d=0, т.е. и

Поставим матрицу С в замену:

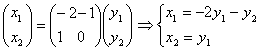
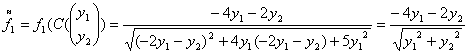
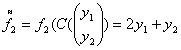
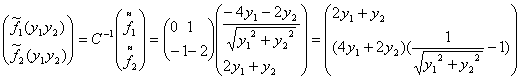
Подставим полученные значения в систему (2):

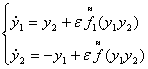
, где

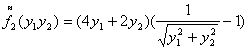
При получаем систему

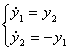
Это уравнение малых колебаний маятника. По теореме о дифференцируемости по параметру при малых e решение (на конечном интервале времени) отличается поправкой порядка e от гармонических колебаний:

Следовательно, при достаточно малом e = e(Т) фазовая точка остается вблизи окружности радиуса А в течении интервала времени Т.

При фазовая кривая не обязательно замкнутая: она может иметь вид спирали, у которой расстояние между соседними витками очень мало (порядка e). Чтобы узнать, приближается ли фазовая кривая к началу координат или уходит от него, рассмотрим приращение энергии 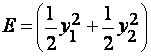за один оборот вокруг начала координат. Нас интересует знак этого приращения: на раскручивающейся спирали приращение положительное, на сжимающейся – отрицательное, а на цикле равно 0. Выведем приближенную формулу:

Подставляя значения и , получим:

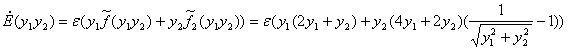
Для вычисления энергии за оборот следовало бы проинтегрировать эту функцию вдоль витка фазовой траектории, которая неизвестна. Но виток близок к окружности. Поэтому интеграл можно посчитать с точностью до O() по окружности радиуса А.

Пусть , тогда

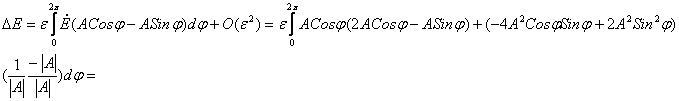
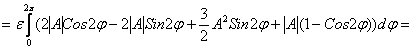
для (при малых положительных значениях ), поэтому фазовые точки удаляются от центра, т.е. фазовая кривая раскручивается.

Вектор скорости кривой направлен по часовой стрелке, так как точка с координатами (1,0) переходит в точку (0,-1)

Так как detC>0, то при замене на ориентация системы координат не изменилась.

Литература

1. Лизоркин Г.И. Курс обыкновенных дифференциальных и интегральных уравнений. М.: Наука, 1981, Гл.7. §6. С.344-348.

2. Эльсгольц Г.Э. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969, Гл.2. §7.

3. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1969, Гл.1. §5.

4. Болтянский В.Г. Математические методы оптимального управления. М.: Наука, 1969, Гл.1. §3.

5. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М.: Наука, 1974, Гл.2. §16.