Теорема продолжимости для спектральных функций плотности : Если каждая окрестность каждой точки в К имеет строго положительную меру , то

1/если равномерно ограничено от нуля по К, то

,

2/если , то

для некоторых непрерывных, строго положительных функций .

Доказательство : Первое утверждение может быть доказано посредством рассмотрения отображения ограниченной функции на вектор , определяемый путем

(А1)

То, что имеет равномерное ограничение от ноля означает, что для некоторого для всех . Поскольку Функции являются линейно-незазисимыми функциями на К и, так как каждая окрестность каждой точки в К содержит множество со строго положительной мерой, то отсюда следует, что отражением множества ограниченных -полиномов

(А2)

при /A1/, является окрестность О. Поэтому отражением

(А3)

является подмножество Е, которое находится в окрестности .

Следовательно, .

Второе утверждение может быть доказано посредством рассмотрения множества корреляционных векторов, соответствующих функциям спектральной плотности, которые являются интегрируемыми, непрерывными и строго положительными /следовательно, с ограничением от нуля/,

является выпуклым и, из доводов, приведенных выше, следует, что - открыто. Легко показать., что векторы для находятся в замыкании . Из теоремы Каратеодори [16] следует, что каждый может быть записан в виде положительной суммы 2М + I таких . Поскольку каждый находится в замыкании , то отсюда следует, что каждый находится там же. Поэтому замыканием является Е. Два открытых выпуклых множества с одинаковым замыканием должны быть идентичными. Поскольку Е находится в замыкании как , так и , то отсюда следует, что

Приложение В

Теорема представления

Теорема представления раздела IУ-А является простым распространением теоремы Каратеодори [16] для корреляционных векторов на границе Е с использованием теоремы о продолжимости. Это обобщение "теоремы С" Каратеодори [9, гл. 4] для многократных измерений. Ввиду вывода метода Писаренко в разделе 1У, как линейной программы, теорема представления может также рассматриваться, как вид фундаментальной теоремы линейного программирования. [l8].

Теорема представления: Если находится на границе Е, то для некоторых 2М неотрицательных и некоторых :

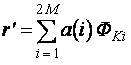(В1)

Доказательство: Рассмотрим компактное выпуклое множество , которое является выпуклой оболочкой . По теореме Каратеодори,. любой элемент в Е может быть выражен в виде выпуклой комбинации 2М+1 элементов А

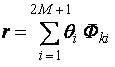(B2)

при и . Если одно из равно нулю, доказательство завершено. Иначе, поскольку находится на границе , имеется некоторый ненулевой , такой что

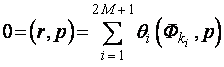(В3)

Итак, для каждого , должны быть линейно зависимыми, следовательно имеются некоторые , не все нули, так что . Пусть является числом с наименьшим значением, так что для некоторого .

Тогда

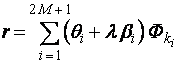(B4)