Объект A обладает свойствами c1, c2, …, cn.

Объект B обладает свойствами c1, c2, …, cn-1.

Предполагается, но не утверждается, что B обладает свойством cn. Именно поэтому аналогию нельзя считать доказательным методом, ее еще надо обосновать. Тем не менее, рассуждения по аналогии полезны в процессе обучения, так как подразумевают самостоятельную формулировку новых теоретических фактов. Основная ошибка школьников при применении аналогии – это отсутствие рассуждений, которые бы полностью ее обосновывали. Без них решение является неполным или просто неверным.

Рассмотрим наиболее часто встречающиеся в решениях школьников виды необоснованных аналогий:

1) Расширение сферы применения теоремы. Появление такого рода ошибки, как правило, связано с формальным знанием теоремы или свойства. В сознании ученика четко не выделены условия применимости теоремы, и в результате некоторые из них остаются за пределом его рассмотрения. Следствием этого является незаконное использование теоремы. По сути ученик применяет не теорему, а ее аналог, который нередко оказывается неверным. Рассмотрим пример:

Пример Aн1: Хорда, не проходящая через центр окружности, равна диаметру.[5]

Доказательство: Дана окружность с диаметром AB. Выберем на ней произвольно точку C. Середина AC – точка D. Проведем через точки B и D хорду BE.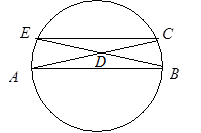 Теперь соединим точки C и E.

Рассмотрим треугольники ADB и DCE. Они равны по стороне и двум углам: AD = DC по построению; ÐB = ÐC как вписанные, опирающиеся на одну дугу AE; ÐADB = ÐCDE как вертикальные. Значит соответствующие стороны AB и EC равны.

Анализ ошибки: «Равенство треугольников по стороне и двум углам» – именно такую условную формулировку часто дают признаку равенства треугольников по стороне и прилежащим к ней углам. В результате школьники просто ищут пары равных элементов: AD = DC, ÐB = ÐC, ÐADB = ÐCDE. При этом условие, что углы должны быть прилежащими соответственно к сторонам AB и DC, забывается. Буквальное восприятие условной формулировки признака равенства треугольников приводит к замене его совсем другим. Произошло расширение сферы применения признака. Ученик воспользовался им без выполнения надлежащих условий, он заменил их на более общие. Это и привело к противоречивому факту – равенству хорды, не проходящей через центр, диаметру. В этом случае лучше всего будет, если ученик самостоятельно, просмотрев предварительно точную формулировку признака равенства треугольников, найдет у себя ошибку.

2) Использование вместо теоремы обратного к ней утверждения. Смысл рассуждений при этом заключается в следующем: если у нас верно AÞB, то верным будет и BÞA. Понятно, что это выполняется не всегда. Приведем простой пример, когда обратная теорема не верна, и ее применение приводит к противоречивому результату.

Пример Ан2: Докажем, что все числа равны.

Для этого возьмем два произвольных числа a и b. Докажем, что a = b.

0 = 0 Þ a2 – 2ab +b2 = b2 –2ab + a2 Þ (a – b)2 = (b – a)2 Þ a – b =

= b – a Þ 2a = 2b Þ a = b.

Переход (a – b)2 = (b – a)2 Þ a – b = b – a не верен. Дело в том, что из равенства чисел следует равенство их квадратов, но из равенства квадратов не следует равенство чисел (будут равны лишь их модули).

3) Ошибки при попытке обобщения. Пусть у нас имеется класс A и класс B. Для элементов класса A выполняется свойство CA. Делается предположение, что для элементов класса B будет выполняться условие CB, которое построено по аналогии со свойством CA в соответствии с особенностями класса B. Например:

Задача Ан3: В прямом параллелепипеде ребра равны a, b, c. Найдите длину главной диагонали.

Решение: Так как в прямоугольнике квадрат диагонали равен сумме квадратов его сторон, то квадрат главной диагонали в прямом параллелепипеде будет равен сумме квадратов его ребер, то есть a2 + b2 +c2.

В данном случае утверждение, полученное по аналогии, верно, но не доказано.

Другой пример: в плоскости любая прямая задается уравнением вида Ax + By + C = 0. Предположение, что в пространстве любая прямая будет задаваться уравнением вида Ax + By + Cz + D = 0 не верно.

Задача учителя – объяснить ученику, что утверждение, полученное по аналогии с верным, может оказаться неверным. Поэтому оно требует отдельного доказательства.

1.4 Абстракция, конкретизация и обобщение.

Абстракция состоит в том, что субъект, вычленяя какие-либо свойства, признаки изучаемого объекта, отвлекается от остальных [2]. Абстрагирование, процесс применения абстракции, обычно осуществляется в результате анализа. При этом признак, отделяемый от объекта, становится самостоятельным объектом мышления.

Конкретизация предполагает возвращение мысли от общего и абстрактного к конкретному с целью раскрыть его содержание [2].

Обобщение – мысленное объединение предметов и явлений по их общим и существенным признакам [2].

Эти три процесса тесно взаимосвязаны между собой. Абстрагирование, как правило, происходит лишь после обобщения, когда объект абстрагирования выделен. Конкретизация – процесс, обратный к абстрагированию.

Обобщение можно определить, как переход от единичного к общему. Рассматриваются конкретные объекты класса. У этих объектов замечается выполнение определенного свойства, делается предположение, что для всех объектов класса это свойство будет выполняться. На самом деле есть определенная схожесть с аналогией, но есть и отличие: при обобщении мы можем с помощью абстрагирования работать с классом, как с одним объектом. Например, любое число, делящееся на 5 можно представить в виде 5k. Доказав какое-то свойство для этого объекта, мы тем самым докажем это свойство для всего класса. Обратное происходит при конкретизации: если свойство верно для всего класса, то для конкретного объекта этого класса свойство будет выполняться.

Рассмотрим ошибки, которые могут возникать при этих процессах.

Одна из распространенных ошибок – необоснованность обобщений. Свойство класса при этом просто замечается, но не доказывается, оно, как правило, проверяется лишь для нескольких элементов класса. Рассмотрим классический пример, принадлежащий Л. Эйлеру:

Пример О1: Верно ли, что при любом натуральном n n2 + n +41 – простое число?

Доказательство: при n = 1: n2 + n + 41 = 43 – простое число;

при n = 2: n2 + n + 41 = 47 – простое число;

при n = 3: n2 + n + 41 = 53 – простое число;

при n = 4: n2 + n + 41 = 61 – простое число;

при n = 5: n2 + n + 41 = 71 – простое число;

и т. д. При остальных n выражение n2 + n + 41 также будет простым числом.

Обобщение в этом случае не только не обосновано, но и опровергается конкретным примером: при n = 41 имеем n2 + n + 41 = 412 + 41 + 41 = 41×(41+2) = 41×43.

В жизни обычно на основе проверки свойства у нескольких объектов класса делается вывод, что данное свойство выполнимо для всего класса в целом. Примерно так строилось большинство физических законов; на ограниченном числе опытов выводились биологические и химические закономерности. Конечно, обобщение – это неотъемлемая часть построения гипотез. Но именно гипотез, из которых лишь впоследствии вырастают логически обоснованные теории. Из рассмотренного выше примера видно, что проверенное даже на многих конкретных примерах утверждение (для натуральных чисел, меньших 41, оно выполняется) может оказаться ложным. Подобные ситуации и вынуждают приводить полные доказательства полученных обобщений, независимо от степени уверенности в справедливости данной гипотезы.