(7)

Решить уравнения

F(X)=0,

значит найти такую точку X(K+1), в которой F[X(K+1)] обращается в нуль. Поэтому, приравнивая левую часть в разложении (7) нулю, получим итерационную формулу для метода Ньютона:

(8)

Применение в этой процедуре обратной матрицы Якоби УРР не означает, что ее необходимо получать на каждой итерации в явном виде. Действительно, перепишем (8) в следующем виде

; (9)

, (10)

где DX(k) – вектор поправок.

Вычисление DX(k) связано с решением системы линейных уравнений (10), что не требует прямого обращения матрицы Якоби.

Решение линейной системы (10) требует меньших ресурсов ЭВМ, чем обращение матрицы, поэтому в практике расчетов используется, как правило, итерационная формула (9).

В случае монотонности функции f(x) метод обеспечивает получение решения с любого приближения. Если функция немонотонная, то получение решения существенно зависит от начального приближения. Метод может «проскочить» интересующее решение и выйти к другому, или вообще разойтись.

Таким образом, обладая быстрой и надежной сходимостью вблизи решения, метод Ньютона очень чувствителен к выбору начальных приближений, что является одним из его недостатков. Второй недостаток обусловлен необходимостью решения систем линейных уравнений на каждой итерации. При использовании стандартных алгоритмов решения СЛУ требуемый объем памяти для хранения матрицы коэффициентов пропорционален квадрату, а время отсчета – кубу, числа узлов рассматриваемой электрической системы. Даже современные ЭВМ были бы не в состоянии обеспечить в этом случае расчет сложных электрических систем, содержащих сотни узлов.

По указанным причинам метод Ньютона долгое время не находил широкого применения для расчетов режимов. Только в результате разработки модификаций метода, обеспечивающих более стабильную сходимость итерационного процесса, и использования вычислительных схем СЛУ, эффективно учитывающих слабую заполненность матрицы Якоби, рассмотренные недостатки удалось преодолеть. В настоящее время метод Ньютона реализован в большом числе программ, предназначенных для расчетов режимов сложных ЭС.

Модификация метода Ньютона, использованная в работе [28] для реализации способа непрерывного утяжеления, основана на использовании итерационной процедуры вида [2]:

, (11)

где 0 < lk £ 1 – корректирующий коэффициент, определяющий величину шага и выбираемый на основе соотношений

ì1/Вk, если Bk > 1;

lk= í (12)

î1, если Вk £ 1,

где

- модуль максимальной невязки;

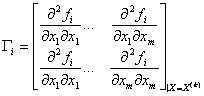
- матрица Гессе от функции fi (x), вычисленная в точке X(k).

Второй сомножитель для Вk представляет собой максимальный по модулю элемент вектора, полученного в результате умножения матрицы вторых производных вектор-функции F(X) на компоненты вектора поправок DX(k). доказано, что если не происходит вырождение матрицы , итерационная процедура (11) обеспечивает сходимость вычислительного процесса для любых существующих режимов вплоть до предельных, а при расчете несуществующих режимов процесс вычислений сходится к точке предельной гиперповерхности, где Якобиан системы УРР (предполагается, что пределы передаваемой мощности и устойчивости равны, т.е. вектор-функции F(X,Y) и W(X,Y) совпадают) равен нулю.

Суть способа непрерывного утяжеления можно пояснить на ходе итерационного процесса на плоскости двух параметров Y1 и Y2. При этом исходному режиму соответствует точка (Y1(0), Y2(0)), а утяжеление осуществляется изменением параметра Y2, то есть

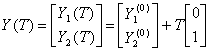
Начальная величина параметра Т выбирается таким образом, чтобы выйти за пределы области устойчивости (существования рушения). После первой итерации происходит переход в точку, где вследствие неучета нелинейных членов разложения функции F(X,Y) в ряд Тейлора, кроме невязок по утяжеляемому параметру (Y2(н)-Y2(1)) появляется невязка по другой координате (Y1(1)-Y1(0)). По этой причине на второй итерации направление утяжеления изменяется, осуществляется переход в точку, где также имеет место отклонение от выбранной траектории Y(T), изменение направления утяжеления и т.д. При достижении предельной поверхности LF (LW) из-за наличия результирующих невязок по параметру Y1, не являющемуся утяжеляемым, возникает несоответствие между полученной точкой и искомой точкой. Поэтому появляется необходимость в уточнении решения. При этом вычислительный процесс, на каждой итерации которого невязка по утяжеляемому параметру полагается нулевой, проходит вблизи предельной поверхности, где матрица плохо обусловлена.

Можно обойтись без процесса уточнения одним из следующих способов.

Первый из них основан на дополнительной балансировке неутяжеляемых параметров режима при выходе их за пределы допустимых значений.

Другой способ связан с дополнительным, по сравнению с выбранным (11) , уменьшением шага. Этим обеспечивается требуемая степень соответствия результирующей точки вычислительного процесса и искомой предельной точки.

Однако, обе рассмотренные модификации приводят к нежелательному увеличению количества итераций. Общей причиной указанных осложнений является линеаризация УУР при использовании итерационной процедуры (11). Указанный недостаток можно устранить с помощью применения вычислительных методов [14, 29], которые позволяют увеличить шаг в выбранном направлении при обеспечении заданной точности по неутяжеляемым параметрам.

Они основаны на дополнительном учете нелинейных членов разложения в ряд Тейлора вектор-функции

обратной к F(X). Благодаря этому удается обеспечить такой ход итерационного процесса, при котором невязки по параметрам, не входящим в число утяжеляемых, всегда остаются в пределах допустимых значений.

Существенным преимуществом методов непрерывного утяжеления является их быстродействие и отсутствие необходимости в выборе величины шага утяжеления. Однако при этом не снимаются вычислительные сложности, связанные с вырожденностью матрицы Якоби УУР в точке решения.

2.3. Применение уравнений предельных режимов

для определения параметров Xпр, Yпр

В работах [30, 31, 31, 33] предложено применить уравнения предельных режимов, которые дают аналитическое описание гиперповерхности предельных режимов. Существенным свойством этих уравнений является невырожденность отвечающей им матрицы Якоби в точке решения. Этим снимаются трудности с решением плохо обусловленных СЛУ.