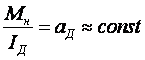Аналитическое определение некоторых механических параметров конструкции электропривода протеза

Рефераты >> Технология >> Аналитическое определение некоторых механических параметров конструкции электропривода протеза

Аналитическое определение некоторых механических параметров конструкции электропривода протеза

К числу наиболее важных параметров электропривода протеза содержащего микроэлектродвигатель и редуктор, можно отнести момент и скорость вращения вала, развиваемые двигателем в нормальном режиме; момент инерции вращающихся масс; передаточное число редуктора; вес; габариты и др. Причем передаточное число редуктора влияет на величину момента электродвигателя, идущую на преодоление сил сопротивления. Изменение скорости при этом влечет за собой и изменение кинетической энергии двигателя. Известно, что динамические параметры двигателей определяют их габариты и вес. Таким образом, для заданного режима движения имеется какое-то оптимальное передаточное число редуктора, при котором электродвигатель, выбранный из определенной серии, имеет минимальные размеры и вес, а также наиболее подходящие с точки зрения энергоэкономичности и быстродействия характеристики.

Задаче совместного определения параметров электродвигателя и оптимального передаточного числа редуктора, относящейся к классу задач вариационного исчисления при поиске экстремали, посвящено значительное число работ. Как указывают многие авторы, в большинстве существующих приводных систем электрические и динамические характеристики элементов, из которых состоит система, недоиспользуются. Неправильный выбор передаточного числа и характеристик двигателя может существенно снизить эффективность управления, а следовательно, и качество функционирования проектируемой системы, так как от них зависит электромеханическая постоянная времени постоянная времени интегрирования, в основном, определяющие время переходных процессов. Привод пристроенный лишь с учетом требуе­мых моментов, имеющие небольшие размеры, становится трудноуправляемым в режимах слежения, имеет низкую производительность.

Как правило, за критерий оптимальности выбора принимает максимальное быстродействие, которое определяет производительность, но с учетом ограничений по току, нагреву и т. д. Однако многообразие приемов и методик определения механических параметров двигателя редуктора уже по одному этому критерию указывает на то, что в каж­дом отдельном случае существуют частные условия оптимизации, обус­ловленные спецификой работы исполнительного механизма. Это приво­дит к тому, что выражения, справедливые при решении одних задач, требуют дополнительных исследований для применения их к другим конкретным задачам.

Рассмотрим электропривод протеза, работающий в повторно-крат­ковременном режиме, удовлетворительно охлаждаемый, управляемый заданным образом. Нужно при заданных моменте сопротивления ис­полнительного механизмаи моменте инерции Iм найти такое опти­мальное передаточное число редуктора k0, при котором обеспечивается требуемое перемещение исполнительного механизма в заданное время t0 с минимальным моментом двигателя МД и весом.

Введем следующие допущения: потери в редукторе учитываются как постоянные (не зависящие от передаточного числа и скорости): мо­ментом инерции редуктора пренебрегаем ввиду его незначительной ве­личины (10—15%) от момента инерции электродвигателя IД): момент сопротивления не зависит от перемещения. Отметим также, что влияние числа оборотов двигателя на уровень акустического шума привода не учитывается.

С учетом допущений можно записать следующее уравнение равно­весия моментов двигателя с редуктором, приведенных к залу исполни­тельного механизма:

(1)

где k — передаточное число редуктора,

— угловая скорость движения исполнительного механизма,

t — текущее время,

— кпд редуктора.

Считая величины и заданными, за единицу скорости во время работы принимаем среднюю скорость

(2)

Запишем уравнение (1) в относительных единицах, приняв за еди­ницу момента

(3)

Разделив все члены уравнения (1) на и обозначив

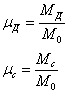(4, 5)

получим выражение

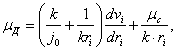
где

Известно [6], что если момент изменяется в процессе работы, то в расчет принимается эквивалентный момент сопротивления, величина которого определяется как среднее квадратическое отдельных значений. В нашем случае, в относительных единицах, эквивалентный момент будет определяться:

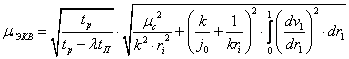(6)

где — коэффициент, учитывающий охлаждение электродвигателя во время паузы,

— время паузы.

Полагаем, что скорость () в конце и в начале перемещения равна нулю:

(0)= (0)=0

Так как момент и скорость, развиваемые двигателем. пропорциональны току в обмотке якоря, a интеграл от квадрата тока по времени — выделяющемуся теплу, то, согласно [7],

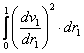=А (7)

где А — параметр тепловыделений по току в якоре, зависящий от формы диаграммы скорости или тока (т. е. от режима управления) и выраженный в относительных единицах.

Установлено [7], что при оптимальном управлении электродвигателем скорость его изменяется по параболе и А = 12 (линейная диаграмма тока). Для любой другой диаграммы А>12. Однако всякая реальная система может обеспечить только известное приближение к оптимальному закону. Как правило, электропривод протеза имеет импульсный характер питания (прямоугольная диаграмма тока) и А = 13.5.

Поскольку в величину выражения (6) входит IД и она зависит от величины (соответствующей значению номинального моменте двигателя Мн. по которому он выбирается из серии), то на первом этапе приближения исходим из предположения, что для данной серии дви­гателей отношение