В теории вероятностей встречаются несколько с иным типом зависимости - вероятностной зависимостью. Если величина Y связана с величиной Х вероятностной зависимостью, то, зная значение Х, нельзя точно указать значение Y, а можно указать её закон распределения, зависящий от того, какое значение приняла величина Х.

Вероятностная зависимость может быть более или менее тесной; по мере увеличения тесноты вероятностной зависимости она все более приближается к функциональной. Т.о., функциональную зависимость можно рассматривать как крайний, предельный случай наиболее тесной вероятностной зависимости. Другой крайний случай - полная независимость случайных величин. Между этими двумя крайними случаями лежат все градации вероятностной зависимости - от самой сильной до самой слабой.

Вероятностная зависимость между случайными величинами часто встречается на практике. Если случайные величины Х и Y находятся в вероятностной зависимости, то это не означает, что с изменением величины Х величина Y изменяется вполне определенным образом; это лишь означает, что с изменением величины Х величина Y

имеет тенденцию также изменяться (возрастать или убывать при возрастании Х). Эта тенденция соблюдается лишь в общих чертах, а в каждом отдельном случае возможны отступления от неё.

Примеры вероятностной зависимости.

Выберем наугад одного больного с перитонитом . случайная величина Т - время от начала заболевания, случайная величина О - уровень гомеостатических нарушений. Между этими величинами имеется явная зависимость, так как величина Т является одной из наиболее главных причин, определяющих величину О.

В то же время между случайной величиной Т и случайной величиной М, отражающей летальность при данной патологии, имеется более слабая вероятностная зависимость, так как случайная величина хоть и влияет на случайную величину О, однако не является главной определяющей.

Тем более, если рассматривать величину Т и величину В (возраст хирурга), то данные величины практически независимы.

До сих пор мы обсуждали свойства систем случайных величин, давая только словесное разъяснение. Однако существуют числовые характеристики, посредством которых исследуются свойства как отдельных случайных величин, так и системы случайных величин.

Одной из важнейших характеристик случайной величины нормального распределения является математическое ожидание.

Рассмотрим дискретную случайную величину Х, имеющую возможные значения Х1, Х2, . , Хn с вероятностями р1, р2, . , рn. нам требуется охарактеризовать каким-то числом положение значений случайной величины на оси абсцисс с учетом того, что эти значения имеют различные значения. Для этой цели обычно пользуются так называемым "средним взвешенным" из значений Хi, причем каждое значение Хi при осреднении должно учитываться с "весом", пропорциональным вероятности этого значения. Таким образом, если обозначить "среднее взвешенное" через М[X] или mx, получим

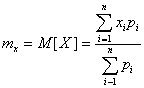
или, учитывая, что , то

(1).

Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.

Для большей наглядности рассмотрим одну механическую интерпретацию введенного понятия. Пусть на оси абсцисс расположены точки с абсциссами х1, х2, …, хn, в которых сосредоточены соответственно массы р1, р2, … , рn, причем . Тогда математическое ожидание есть не что иное, как абсцисса центра тяжести данной системы материальных точек.

Формула (1) для математического ожидания соответствует случаю дискретной случайной величины. Для непрерывной величины Х математическое ожидание, естественно, выражается не суммой, а интегралом:

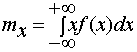
(2),

где - плотность распределения величины Х.

Формула (2) получается из формулы (1), если в ней заменить отдельные значения Хi непрерывно изменяющимся параметром Х, соответствующие вероятности рi элементом вероятности f(x)dx, конечную сумму - интегралом.

В механической интерпретации математическое ожидание непрерывной случайной величины сохраняет тот же смысл - абсциссы центра тяжести в случае, когда масса распределения по оси абсцисс непрерывна с плотностью f(x).

Следует отметить, что математическое ожидание существует не для всех случайных величин, что, однако, по мнению некоторых ученых, не представляет для практики существенного интереса.

Помимо математического ожидания важное значение имеют также другие числовые случайной величины - моменты.

Понятие момента широко применяется в механике для описания распределения масс ( статистические моменты, моменты инерции и т.д.). Совершенно теми же приемами пользуются в теории вероятностей для описания основных свойств распределения случайной величины. Чаще всего применяются на практике моменты двух видов: начальные и центральные.

Начальным моментом s-го порядка прерывной случайной величины Х называется сумма вида

Очевидно это определение совпадает с определением начального момента порядка s в механике, если на оси абсцисс в точках х1, …, хn сосредоточена масса р1, …, рn.

Для непрерывной случайной величины Х начальным моментом s-го порядка называется интеграл

Очевидно, что

,

т.е. начальный момент s-го порядка случайной величины Х есть не что иное, как математическое ожидание s-ой степени этой случайной величины.

Перед тем как дать определение центрального момента введем понятие "центрированной случайной величины".

Пусть имеется случайная величина Х с математическим ожиданием mx. Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от её математического ожидания

Нетрудно видеть, что математическое ожидание центрированной случайной величины равно нулю.

Центрирование случайной величины равносильно переносу начала координат в точку, абсцисса которой равна математическому ожиданию.

Центральным моментом порядка s случайной величины Х называется математическое ожидание s-ой степени соответствующей центрированной случайной величины:

.

Для прерывной случайной величины s-й центральный момент выражается суммой