Найдем мат.ожидание случайной величины Z.

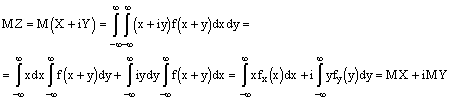
1. Для комплексной случайной величины справедливы свойства аддитивности и мультиплекативности мат.ожидания.

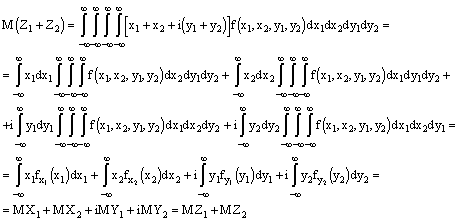
2. Комплексные случайные величины Z1 и Z2 называются независимыми, если независимы между собой двумерные случайные величины , т.е. попарно независимы

Пусть Z1 и Z2 независимые комплексные случайные величины. Найдем мат.ожидание произведения

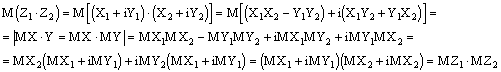
3.

а) дискретный случай

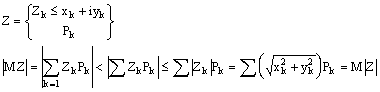
б) непрерывный случай

Двумерная случайная величина XY имеет плотность вероятности f(x,y).

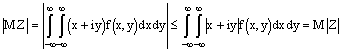
Характеристической функцией действительной случайной величины X называется функция

Свойства характеристической функции

1. Для дискретного случая

2. Для непрерывного случая

Будем считать, что плотность вероятности f(x) существует, тогда

3.

Это свойство гарантирует, что характеристическая функция всегда существует

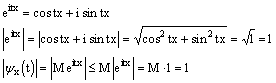
4. Пусть случайная величина

y=ax+b

5. Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций.

Пусть

хi - независимы

Тогда

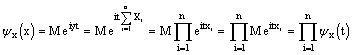
Отсюда

6. Если у случайной величины Х конечен начальный момент n-го порядка, то

а) для - существуют к-е производные и при этом

б) имеет место разложение

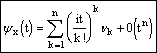
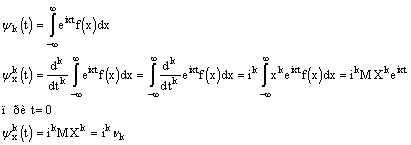
Для того, чтобы полученное равенство было справедливо, необходимо доказать, что мы можем дифференцировать под знаком интеграла.

Для доказательства приведем ряд фактов.

1. Аналог теоремы Либега для интегралов Римана

Пусть функция интегрируема по Риману и при всех х

сходимость в каждой точке известна.

Пусть при этом

- некоторая функция, мажорирующая данную. Пусть при этом конечен интеграл

т.е.

Тогда

2. Некоторые свойства мат.ожиданий действительной случайной величины

1) Если х>0, то МХ>0 - доказать самим

Дискретный случай

Введем случайную величину

Аналогично

Очевидно, что

Следовательно

Тогда

Пара может принимать значения:

а) (-¥,+¥) в этом случае говорится, что МХ не определено.

б) (-¥,<¥) в этом случае говорится, что МХ не ограничено.

в) (<¥, ¥) MX=-¥

(<¥, <¥) MX<¥

Очевидно, что

Вывод:

Если MX конечно, то конечно и M/X/

MX<¥, то M/X/<¥

Если MXk конечно, то конечно и M/Xk/

MXk<¥, то M/Xk/<¥

3. Пусть , тогда

на основании пункта 1.

4. Имеет место очевидное неравенство

5. Пусть существует , тогда для всех

Сумма интегралов

Возвращаемся к доказательству.

Докажем формулу

Доказательство проведем по мат.индукции.

Проверяем при k=0

формула справедлива.

Пусть формула справедлива для k<n. Докажем, что она справедлива для k+1.

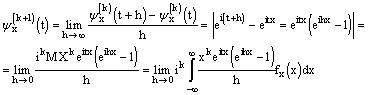
Рассмотрим.

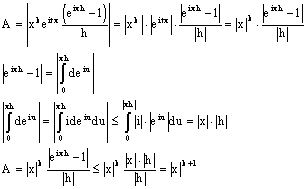
Получили:

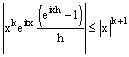
Покажем, что интеграл конечен.

Если , то и конечно. А конечно по условию, тогда для

Таким образом можно применять теорему Либега.

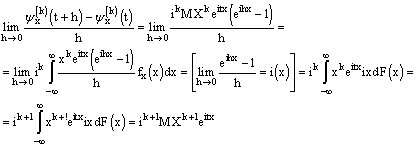
Это мы доказали справедливость формулы