Другими словами, репрезентативность выборки обеспечивается случайностью отбора объектов в выборку.

Существует несколько способов отбора, обеспечивающих репрезентативность выборки.

Пусть небольшие по размеру объекты генеральной совокупности находятся, например, в ящике. Каждый раз после тщательного перемешивания (если оно не вызывает разрушение объектов) из ящиков наудачу берут один объект. Эту операцию повторяют до тех пор, пока не образуется выборка нужного объема. Очевидно, что такая техника отбора невозможна, если генеральная совокупность состоит из больших (по размерам) или хрупких объектов. В этих случаях поступают следующим образом. Все объекты генеральной совокупности нумеруют и каждый номер записывается на отдельную карточку. После этого карточки с номерами тщательно перемешиваются и из пачки карточек выбирают одну. Объект, номер которого совпал с номером выбранной карточки, включается в выборку. Номера объектов можно "отбирать" с помощью таблиц случайных чисел – это целесообразно при большом объеме генеральной совокупности.

1.3. Вариационные ряды

После получения (тем или иным способом) выборочной совокупности все ее объекты обследуются по отношению к определенной случайной величине – т.е. обследуемому признаку объекта. В результате этого получают наблюдаемые данные, которые представляют собой множество расположенных в беспорядке чисел. Анализ таких данных весьма затруднителен, и для изучения закономерностей полученные данные подвергаются определенной обработке.

¨Пример. На телефонной станции проводились наблюдения над числом Х неправильных соединений в минуту. Наблюдения в течение часа дали следующие 60 значений:

3; 1; 3; 1; 4; ï 2; 2; 4; 0; 3; ï 0; 2; 2; 0; 2; ï1; 4; 3; 3; 1;

4; 2; 2; 1; 1; ï 2; 1; 0; 3; 4; ï 1; 3; 2; 7; 2; ï0; 0; 1; 3; 3;

1; 2; 4; 2; 0; ï 2; 3; 1; 2; 5; ï 1; 2; 4; 2; 0; ï 2; 3; 1; 2; 5.

Очевидно, что число X является дискретной случайной величиной, а полученные данные есть значения этой случайной величины. Анализ ис­ходных данных в таком виде весьма затруднителен.

Численность отдельной группы сгруппированного ряда данных называется частотой , где – индекс варианта, а отношение частоты данного варианта к общей сумме частот называется частностью (или относительной частотой) и обозначается , , т.е.

.

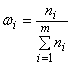Дискретным вариационным рядом называется ранжированная совокупность вариантов с соответствующими им частотами или частностями .

1.5. Выборочное среднее и выборочная дисперсия

Для описания группирования и рассеивания наблюдаемых данных используются так называемые числовые характеристики выборочной совокупности, из которых рассмотрим выборочное среднее [5].

Выборочным средним называется случайная величина, определенная формулой

.

Так как конкретная выборка является реализацией значений случайных величин , то среднее значение выборки

является одной из реализаций случайной величины . Другими словами, есть одно из значений случайной величины .

Если данные представлены в виде вариационного ряда, то целесообразно для вычисления выборочного среднего одно из следующих соотношений:

· для дискретного вариационного ряда

;

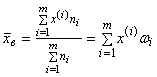· для интервального вариационного ряда

,

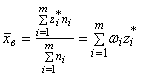где – частность (относительная частота), соответствующая i-й варианте или i-му частичному интервалу; – середина i-го частичного интервала, т.е.

Сравним математическое ожидание дискретной случайной величины Х, вычисляемой по формуле

,

и значение выборочного среднего. Прежде всего, очевидна их внешняя схожесть. Однако в формуле – возможные значения случайной величины, а – вероятности. – варианты случайной величины, полученные в результате наблюдений, – их относительная частота. Далее, математическое ожидание не является случайной величиной, а выборочное среднее – случайная величина, значение которой меняется от выборки к выборке. Несмотря на это, как будет показано ниже, выборочное среднее при определенных условиях выступает как «хорошая» оценка математического ожидания.

2. Точечная оценка математического ожидания

Математическое ожидание генеральной совокупности назовем генеральной средней , т.е.

.

Теорема. Выборочное среднее есть состоятельная и несмещенная оценка генеральной средней .

Доказательство. Вначале покажем, что есть состоятельная оценка для , т.е.