Краевая задача для уравнения смешанного типа с дробной производнойРефераты >> Математика >> Краевая задача для уравнения смешанного типа с дробной производной
Пусть ![]() , где
, где ![]() и
и ![]()
![]() - параболическая и гиперболическая части
- параболическая и гиперболическая части ![]() .
.
Обозначим  , где
, где ![]() .
.
Пусть 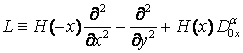 .
.
|
![]()
![]()
|
|
![]() ,
,
где ![]() - непрерывные достаточно гладкие функции, причем
- непрерывные достаточно гладкие функции, причем ![]() .
.
Пусть ![]() .
.
Для доказательства существования решения ![]() задачи А для уравнения (1) в области
задачи А для уравнения (1) в области ![]() , следует решить первую задачу Дарбу
, следует решить первую задачу Дарбу
|
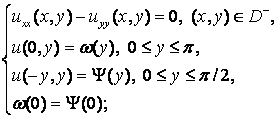
и задачу
|
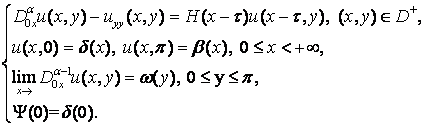
Решение задачи (5) известно (см. курсовую работу) и имеет вид
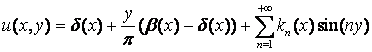 ,
,
где
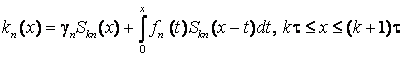 ,
,
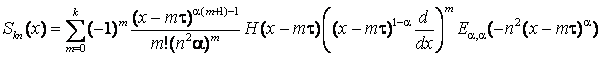 ,
,
а оператор 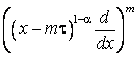 действует следующим образом
действует следующим образом
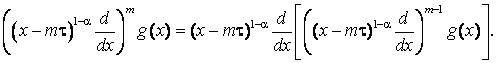
Рассмотрим решение задачи (4).
![]()
![]() уравнение гиперболическое. Рассмотрим характеристическое уравнение
уравнение гиперболическое. Рассмотрим характеристическое уравнение
![]()
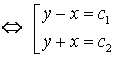 .
.
Сделаем замену переменных
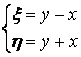 .
.
Учитывая, что
![]() ,
,
![]() ,
,
получим
![]() ,
,
![]() ,
,
а значит
![]() .
.
![]()
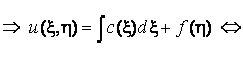
![]() ,
,
получили общее решение гиперболического уравнения ![]() .
.
Используя условия из (4) получим
![]() ,
,
![]() .
.
Таким образом, получили систему уравнений для определения функций ![]() и
и ![]() :
:
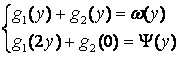 .
.
Из второго уравнения получим
![]()
![]()
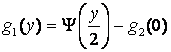 .
.
Из первого уравнения получим
![]()
![]()
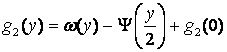 .
.
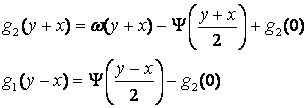
![]()
|
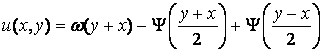
Для определения ![]() используем условие
используем условие ![]() . В силу непрерывности частных производных из гиперболической области
. В силу непрерывности частных производных из гиперболической области ![]() на линии
на линии ![]() получим
получим
|
