Краевая задача для уравнения смешанного типа с дробной производнойРефераты >> Математика >> Краевая задача для уравнения смешанного типа с дробной производной
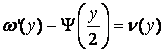 .
.
|
![]() ,
,
и
![]()
![]()
Обозначим
![]() ,
, ![]() .
.
|
![]() ,
, ![]() ,
,
т.е. уравнение
|
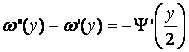
при условиях (9).
Из (10) найдем
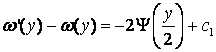 .
.
Общее решение однородного уравнения
![]() .
.
Частное решение ищем в виде
![]() .
.
Подставляя в уравнение найдем
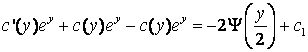 ,
,
т.е.
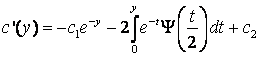 .
.
Поэтому
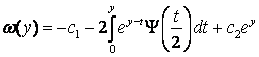 .
.
Т.к.
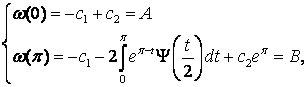
или
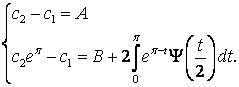
Вычтем из второго уравнения первое
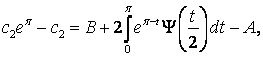
т.е.
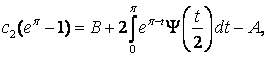
окончательно
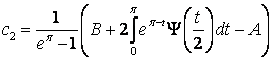 .
.
Для ![]() получим
получим
![]() ,
,
т.е.
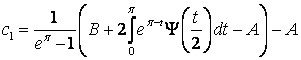 .
.
Таким образом, получили
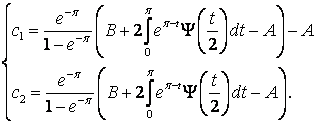
Поэтому

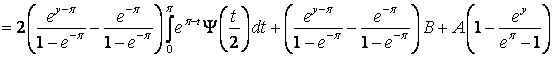 .
.
Тогда для ![]() получим
получим
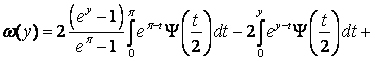
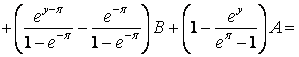
|
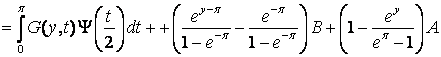 ,
,
где ![]() - функция Грина, определяемая формулой
- функция Грина, определяемая формулой

![]() ,
, ![]() .
.
Решение задачи (4) определяется формулой (6), (11).
Для доказательств единственности решения в области ![]() , докажем, что однородная задача Дарбу имеет только тривиальное решение. Для этого решим задачу (4) при условии:
, докажем, что однородная задача Дарбу имеет только тривиальное решение. Для этого решим задачу (4) при условии: ![]() . Подставляя данные условия в решение полученное на основании формул (6), (11) получим:
. Подставляя данные условия в решение полученное на основании формул (6), (11) получим:
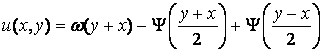 (*)
(*)
т.е. ![]() .
.
Учитывая, что ![]()
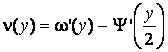 и условие
и условие ![]() , получим
, получим ![]() , что вместе с (8) дает уравнение для определение
, что вместе с (8) дает уравнение для определение ![]() , т.е.
, т.е.
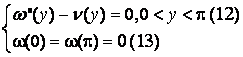
Решение (12) имеет вид:
![]() .
.
С помощью (13) из (14) найдем:
![]()
т.е.
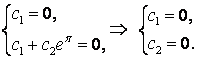
На основании (14) имеем:
![]()
Таким образом, получили, что решение однородной задачи Дарбу может быть только тривиальным. Единственность решения в области ![]() очевидна.
очевидна.
Литература.
1. А.Н. Зарубин Краевые задачи для дифференциальных и дифференциально-разностных уравнений. Орел 2002г.
2. Зарубин А.Н. Уравнения смешанного типа с запаздывающим аргументом. Учебное пособие. – Орел: ОГУ, 1999.
3. А.Н. Тихонов, А.А. Самарский Уравнения математической физики. Москва 1953г.
4. Э. Камке Справочник по дифференциальным уравнениям в частных производных Москва 1967г.
5. Р. Курант Уравнения с частными производными Москва 1961г.
