Интегрирование с помощью подстановки.Рефераты >> Математика >> Интегрирование с помощью подстановки.
![]() **********
**********
4. Опишем около трапеции многоугольник
**********************************
Необходимое условие существование определенного интеграла.
Df. Пусть существует интеграл ![]() подынтегральная ф-ия
подынтегральная ф-ия ![]() ограничена на
ограничена на ![]()
Доказательство:
Пусть ![]() - неограниченна на
- неограниченна на ![]() , то при любом разбиении этого отрезка она неограниченна на каком-то из частичных отрезков Þ ***
, то при любом разбиении этого отрезка она неограниченна на каком-то из частичных отрезков Þ ***![]() на частичном отрезке, мы можем сделать значение ф-ии в т.
на частичном отрезке, мы можем сделать значение ф-ии в т. ![]() сколь угодно большим по модулю Þ интегральная сумма, соотв. этому прозв. разб. будет неограниченна Þ не имеет предела Þ противоречит условию Þф-ия
сколь угодно большим по модулю Þ интегральная сумма, соотв. этому прозв. разб. будет неограниченна Þ не имеет предела Þ противоречит условию Þф-ия ![]() ограничена на
ограничена на ![]()
Некоторые классы интегральных ф-ий.
Df. Любая ф-ия, для которой существует определенный интеграл на ![]() , интегрируема на этом промежутке.
, интегрируема на этом промежутке.
Множество таких ф-ий обозначают ![]()
К интегрируемым на ![]() ф-иям относятся:
ф-иям относятся:
1. Ф-ии, непрерывные на ![]()
2. Монотонные на ![]()
3. Имеющие на отрезке конечное или счетное мн-во точек разрыва 1-го рода.
Свойства определенного интеграла.
Df. Промежуток с гранич. т. A и B ориентированным, если указано направление перехода от т. A к т. B.
1. Пусть сущ. определенный интеграл 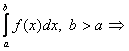 сущ. определенный интеграл
сущ. определенный интеграл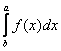 и справедливо равенство
и справедливо равенство
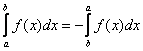
2. 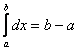
Док-во:
![]()
![]()
3. Свойство линейности определенного интеграла:
1. Пустьф-ии![]() интегрируемы на
интегрируемы на ![]() ***
***
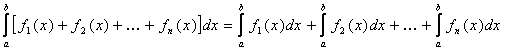
2. Пусть ![]() , то для любой произвольной постоянной
, то для любой произвольной постоянной ![]()
![]() - справедлива формула
- справедлива формула 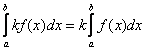
4. Аддитивность определенного интеграла:
Пусть ф-ия ![]() интегрируема на большем их трех помежутков
интегрируема на большем их трех помежутков ![]() , тогда она интегрируема на обоих меньших промежутках и справедлива формула:
, тогда она интегрируема на обоих меньших промежутках и справедлива формула:
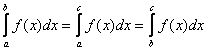
Свойство монотонности.
1. Пусть ф-ия ![]() неотрицательна на
неотрицательна на ![]() и интегрируема на нем,
и интегрируема на нем, 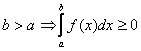
Док-во: В силу н-ва для ф-ий любая интегрируема ф-ия неотрицательна Þ любая последовательность интегрируемых сумм будет иметь неотрицательный предел Þ интеграл будет неотрицательным.
![]()
![]()
2. Пусть ф-ия ![]() на
на ![]() , искл. конечн. точек, и интегрируема на
, искл. конечн. точек, и интегрируема на ![]() , тогда
, тогда 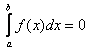
Док-во: Из интегрируемости следует, что предел не зависит от выбора разбиения на ![]() . Достаточно строить инт. разбиения так, чтобы точки, в которых ф-ия равна нулю, являлись точками разбиения. А следовательно в силу аддитивности интеграл по всему прмежутку равен сумме интегралов по частичным промежуткам, т.к ****
. Достаточно строить инт. разбиения так, чтобы точки, в которых ф-ия равна нулю, являлись точками разбиения. А следовательно в силу аддитивности интеграл по всему прмежутку равен сумме интегралов по частичным промежуткам, т.к ****
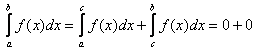
Df Две ф-ии ![]() , заданные на
, заданные на ![]() , значения которых различны на
, значения которых различны на ![]() лишь в конечном ч. точек называются эквивалентными на этом отрезке.
лишь в конечном ч. точек называются эквивалентными на этом отрезке.
3. Инт. от эквивалентных ф-ий совп.
Пусть ![]() эквивалентны и интегрируемы на
эквивалентны и интегрируемы на ![]() , тогда
, тогда 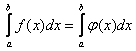 (они не совпадают а интегралы совпадают).
(они не совпадают а интегралы совпадают).
Д-во:
![]() на
на ![]() лишь в конеч. ч. точек отр.
лишь в конеч. ч. точек отр. ![]() , следовательно по 2му
, следовательно по 2му 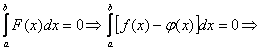
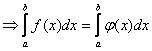
4. Пусть ![]() на
на ![]() , кроме конечного ч. точек,
, кроме конечного ч. точек, ![]() инт. на
инт. на ![]() ,
, ![]() , то
, то 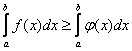
5. Пусть ![]() инт-ма на
инт-ма на ![]() Þ модуль ф-ии тоже интегрируем на
Þ модуль ф-ии тоже интегрируем на ![]() и справедливо неравенство:
и справедливо неравенство:
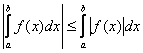
6. Пусть ![]() интегрируема на
интегрируема на ![]() ,
, ![]() , то существует М, такая что
, то существует М, такая что 
