Производная от обратной ф-ии.

Рефераты >> Математика >> Производная от обратной ф-ии.

Dh: Пусть в точке х0 имеет:

1.

2. на промежутке, содержащем х0 , обратную ф-ию

3.

тогда в точке х0 существует , равная

Доказательство:

1. Пустьи двум различным значениям х соответствует е различных значений y .

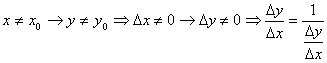
2. Пусть дифф. в точке х0 , тогда

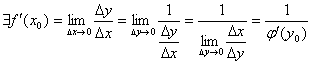
3. т.к.

Производная от сложной ф-ии.

Dh: Пусть:

1. - дифф. в точке y0 .

2. - дифф. в точке х0 .

3.

тогда сложная ф-ия - дифф. в точке х0 и справедлива формула:

Доказательство:

1. - дифф. в точке y0

2. - дифф. в точке х0

3. - дифф. в точке х0 а значит непрерывна в этой точке.

Односторонние производные.

Заменим в определении производной предел – односторонним пределом, получится определение односторонней производной.

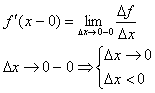
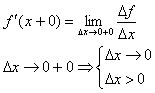
Производная от параметрически заданной ф-ии.

Df: Ф-ия называется заданной параметрически, если ее аналитическое выражение может быть представлено в виде:

t- параметр.

Dh: Пусть ф-ия задана параметрически, где и дифф. в точке х0 , тогда

Доказательство: Предположим. что имеет обратную ф-ию , тогда - сложная ф-ия от х и определению сложной ф-ии имеет:

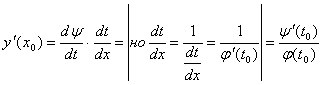
Производные высших порядков.

Df: Пусть ф-ия дифф. на Х , то есть дифф. в каждой т. Х .

Каждому значению Х соответствует единственное значение , т.е. получаем как ф-ию, заданную на Х.

Если она окажется дифф. на Х, то мы можем вычислить следующую , которая будет называться второй и т.д.

Df: Производной n-го порядка от ф-ии называется первая производная от производной n-1 порядка.

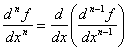
Пример:

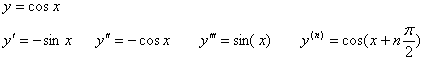
Теоремы о дифф. ф-ях.

Теорема Ферма: Пусть дифф. на и наибольшее или наименьшее ее значение в т. х0 , тогда производная в этой точке равна нулю.

**************************

Доказательство:

Пусть - наибольшее на

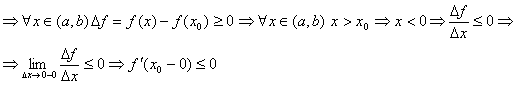
Но из дифф в т. х0

Zm: Из доказательства т. Ферма следует: Пусть непрерывна на промежутке и внутренних точках этого промежутка принимает наибольшее и наименьшее значение, тогда если в этой точке ф-ия дифф., то .

Теорема Ролля: Пусть ф-ия :

1. непрерывна на

2. дифф. на

3. Принимает на концах этого отрезка одинаковые значения.

Тогда на существует т. х0 , в которой

*************

Доказательство:

Из непрерывности ф-ии на отрезке следует, что имеет на этом отрезке свои наименьшее(m) и наибольшее(M) значения.

Возьмем два случая:

1. m=M ; наименьшее значение совпадает с х0 следовательно:

2. ; из (3) следует: ***********

Dh: Между двумя корнями ф-ии есть точка производной.

Теорема Лагранжа: Пусть ф-ия непрерывна на промежутке , дифф. на, тогда на существует такая х0 такая, что верна формула: