Метод СимпсонаРефераты >> Математика >> Метод Симпсона
При выводе правила Рунге вы существенно пользовались предположением, что 
. Если имеется только таблица значений 
, то проверку 
«на постоянство» можно сделать непосредственно по таблице Дальнейшее развитие приведенных алгоритмов позволяет перейти к адаптивным алгоритмам, в которых за счет выбора различного шага интегрирования в разных частях отрезка интегрирования в зависимости от свойств 
уменьшается количество вычислений подынтегральной функции.
Другая схема уточнения значений интеграла - процесс Эйтнена. Производится вычисление интеграла с шагами
, причем 
. Вычисление значений 
. Тогда 
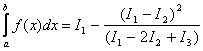(14).
За меру точности метода Симпсона принимают величину :
5. Примеры
Пример 1. Вычислить интеграл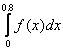 
по формуле Симпсона, если задана таблицей. Оценить погрешность.
Таблица 3.
|
| 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
|
| 1 | 0.995 | 0.98 | 0.955 | 0.921 | 0.878 | 0.825 | 0.765 | 0.697 |
Решение: Вычислим по формуле (1) при 
и 
интеграл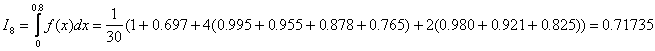 
.
.
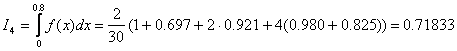По правилу Рунге получаем 
Принимаем 
.
Пример 2. Вычислить интеграл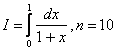 
.
Решение: Имеем 
. Отсюда h=
=0.1. Результаты вычислений приведены в таблице 4.
Таблица 4.
Вычисление интеграла по формуле Симпсона
| i |
|
|
|
| 0 | 0 | y0=1,00000 | |
| 1 | 0.1 | 0,90909 | |
| 2 | 0.2 | 0,83333 | |
| 3 | 0.3 | 0,76923 | |
| 4 | 0.4 | 0,71429 | |
| 5 | 0.5 | 0,66667 | |
| 6 | 0.6 | 0,62500 | |
| 7 | 0.7 | 0,58824 | |
| 8 | 0.8 | 0,55556 | |
| 9 | 0,9 | 0,52632 | |
| 10 | 1,0 | 0,50000=yn | |
| å | 3,45955(s1) | 2,72818(s2) |
По формуле Симпсона получим:
Подсчитаем погрешность полученного результата. Полная погрешность 
складывается из погрешностей действий 
и остаточного члена 
. Очевидно:
