1. Введение . 3

2. Теоретическая часть .4

3. Алгоритм работы 8

4. Код программы .17

· Модуль K_graph 17

· Модуль Graphic .34

· Модуль K_unit .38

· Основная программа 40

5. Тестовые испытания .42

6. Полезные советы по работе с программой .42

7. Окна ввода и вывода программы .

8. Вывод 43

9. Список литературы .44

Математика - одна из самых древних наук. Труды многих ученых вошли в мировой фонд и стали основой современных алгебры и геометрии. В конце XVII в., когда развитие науки шло быстрыми темпами, появились понятия дифференцирование, а вслед за ним и интегрирование. Многие правила нахождения неопределенного интеграла в то время не были известны, поэтому ученые пытались найти другие, обходные пути поиска значений. Первым методом явился метод Ньютона – поиск интеграла через график функции, т.е. нахождение площади под графиком, методом прямоугольников, в последствии усовершенствованный в метод трапеций. Позже был придуман параболический метод или метод Симпсона. Однако часть ученых терзал вопрос: А можно ли объединить все эти методы в один??

Ответ на него был дан одновременно двумя математиками Ньютоном и Котесом. Они вывели общую формулу, названную в их честь. Однако их метод был частично забыт. В этой работе будут изложены основные положения теории, рассмотрены различные примеры, приведены таблицы, полученные при различных погрешностях, и конечно описана работа и код программы, рассчитывающей интеграл методом Ньютона-Котеса.

Пусть некоторая функция f(x) задана в уздах интерполяции:

(i=1,2,3…,n) на отрезке [а,b] таблицей значений:

Требуется найти значение интеграла .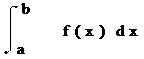

Для начала составим интерполяционный многочлен Лагранджа:

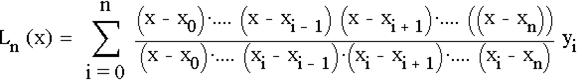
Для равноотстоящих узлов интерполяционный многочлен имеет вид:

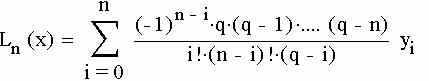
где q=(x-x0)/h – шаг интерполяции, заменим подынтегральную функцию f(x) интерполяционным многочленом Лагранжа:

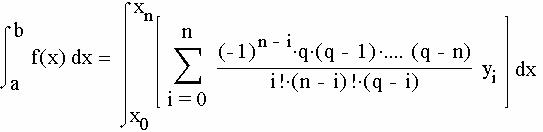
Поменяем знак суммирования и интеграл и вынесем за знак интеграла постоянные элементы:

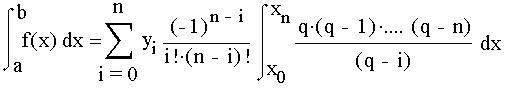
Так как dp=dx/h, то, заменив пределы интегрирования, имеем:

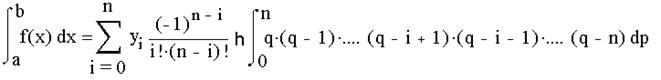
Для равноотстоящих узлов интерполяции на отрезке [a,b] величина шаг определяется как h=(a-b)/n. Представив это выражение для h в формулу (4) и вынося (b-a) за знак суммы, получим:

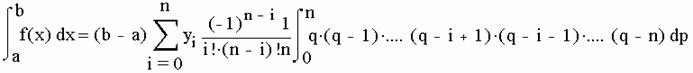
Положим, что

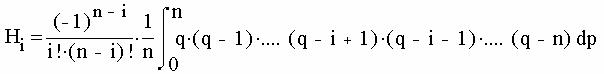
где i=0,1,2…,n; Числа Hi называют коэффициентами Ньютона-Котеса. Эти коэффиценты не зависят от вида f(x), а являются функцией только по n. Поэтому их можно вычислить заранее. Окончательная формула выглядит так:

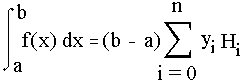
Теперь рассмотрим несколько примеров.

Пример 1.

Вычислить с помощью метода Ньютона-Котаса: 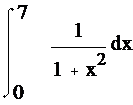, при n=7.

Вычисление.

1) Определим шаг: h=(7-0)/7=1.

2)Найдем значения y:

3) Находим коэффициенты Ньютона-Котеса:

H1=H7=0.0435, H1=H6=0.2040, H2=H5=0.0760 ,H3=H4=0.1730

Подставим значения в формулу и получим:

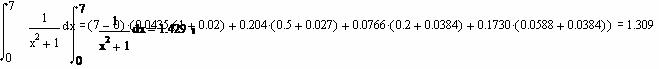При подсчете с помощью формулы Ньютона-Лейбница получим:

Пример 2.

Вычислить при помощи метода Ньютона-Котеса

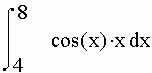, взяв n=5;

Вычисление:

1) Определим шаг h=(8-4)/5=0.8

2) Найдем значения y:

3) Находим коэффициенты Ньютона –Котеса:

H0=H5=0.065972 ;H1=H4=0.260417 ;H2=H3=0.173611 ;

4)Подставим значения в формулу и получим:

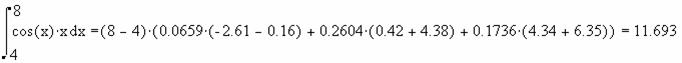
Рассмотрим частные случаи формулы Ньйтона-Котеса.

Пусть n=1 тогда

H0=H1=0.5 и конечная формула примет вид:

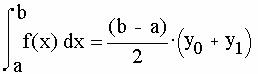Тем самым в качестве частного случая нашей формулы мы получили формулу трапеций.