Критика евклидовского обоснования геометрии, продолжавшаяся на протяжении нескольких веков и ставшая особенно острой в 19 столетии, привела к попыткам нового дедуктивного построения геометрии, отвечающего современным требованиям науки.

Одним из ученых, предвосхитивших неевклидову геометрию, был итальянский монах Джироламо Саккери (1667-1733), преподававший грамматику в иезуитской коллегии в Милане. Здесь под влиянием Джованни Чевы ( Джованни Чева (1648-1734) – итальянский инженер-гидравлик и экономист) Саккери заинтересовался математикой и стал серьезно заниматься ею. Впоследствии он преподавал математику в университете города Павши. На последнем году своей жизни Саккери опубликовал (на латинском языке) книгу под заглавием «Евклид, очищенный от всех пятен». В ней он поставил перед собой задачу исправить все недостатки («пятна») «Начал» Евклида, в первую очередь доказать V постулат. Саккери решительнее и дальше своих предшественников сделал попытку доказать этот постулат от противного. Этот путь он не сумел проделать до конца, но идя по нему, Лобачевский а последствии открыл неевклидову геометрию.

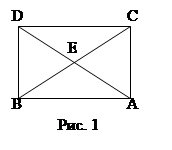Рассматривая четырехугольник (рис. 1), носящий его имя, Саккери стремится доказать, что гипотезы тупого и острого углов приводят к логическим противоречиям и что остается лишь гипотеза прямого угла, из которой вытекает евклидов V постулат. Он легко опровергает гипотезу тупого угла, он доказывает, что:

1. геометрическое место точек плоскости, равноотстоящих от данной прямой по одну сторону, не является прямой или окружностью, а другой линией (которую Лобачевский впоследствии назвал эквидистантой, то есть «равноотстоящей»);

2. две прямые, содержащиеся в одной плоскости (рис. 2), либо пересекаются в одной точке (такие прямые Лобачевский назвал «сходящимися»), либо не пересекаются, имея общий перпендикуляр, по обе стороны от которого они друг от друга удаляются («расходящиеся прямые» в терминологии Лобачевского), либо не пересекаются, удаляясь друг от друга в одном направлении и асимптотически приближаясь в другом (параллельные Лобачевского).

Если бы Саккери пользовался лишь логическими выводами, строгой дедукцией, то никакого противоречия он в указанных выше предложениях не нашел бы. Однако, будучи предубежден о невозможности того, что для евклидова постулата не имелось доказательства, Саккери для опровержения гипотезы острого угла прибег к утверждению чисто интуитивного характера: существование асимптотических прямых якобы «противоречит природе прямой линии». Заслуга Саккери состоит, разумеется, не в конечном его установлении промежуточных предложений, выведенных им на основе гипотезы острого угла, которые 100 лет спустя легли в основу новой неевклидовой геометрии Лобачевского.

К числу предшественников последнего, следует отнести и члена Берлинской Академии наук – астронома, математика и философа Иогана Генриха Ламберта, считавшего себя Швейцарским ученым и писавшего одни из своих произведений на французском языке. Другие – на немецком.

В опубликованном после его смерти произведении «Теория параллельных линий»(1786) Ламберт рассматривает четырехугольник. И исследует, как и Саккери, возможные при этом три гипотезы. Он получает ряд новых результатов геометрии, построенной на гипотезе острого угла, то есть будущей неевклидовой геометрии Лобачевского, в том числе и следующий: если сумма углов треугольника АВС, как известно, меньше двух прямых углов, равна 2d - d, то площадь треугольника пропорциональна d (d - «дефект треугольника»). В отличие от Саккери Ламберт в своих рассуждениях нигде не отступает от строгой дедукции, и поэтому он не находит противоречия в гипотезе острого угла и признает тщетность всех попыток доказать V постулат. Не смотря на это, однако, Ламберт, как и его предшественники, не считал гипотезу острого угла действительно возможной. На таких же позициях стоял и знаменитый французский математик А.М. Лежандр (1752- 1833), значительно способствовавший своими многочисленными попытками доказать евклидову аксиому параллельности, привлечению внимания математиков первой половины 19 в. к проблеме V постулата.

Эта проблема, как известно, была впервые решена профессором Казанского университета, гениальным русским математиком Николаем Ивановичем Лобачевским (1792- 1856), открывшим в 1862 г. первую неевклидову геометрию, называемую так же « гиперболической». Независимо от него к тому же открытию пришел и молодой венгерский математик Я. Бояй. Первый печатный труд по неевклидовой геометрии - статья Н.И. Лобачевского « О началах геометрии» - появился в 1829г. в « Казанском вестнике». Через 3 года была опубликована на латинском языке работа по неевклидовой геометрии « Appendix» («Приложение»), название которой объяснялось тем, что она появилась к одной из работ отца Яноша, математика Фаркаша Бояй. После смерти Гаусса выяснилось, что он также еще до Лобачевского и Бояй пришел к той же геометрии. Идеи Лобачевского и Бояй с трудом пробивали себе дорогу в науке. Лишь в 70-80г.г. прошлого столетия после появления работ Римана, Кэли, Клейта и Пуанкаре более широким кругом математиков стало ясно, что V постулат недоказуем, так как он не зависит от других аксиом евклидовой геометрии.

Попытки доказательства V постулата принесли большую пользу в том отношении, что выяснили, какие теоремы геометрии относятся на этот постулат и какие от него не зависят. Совокупность теорем геометрии, не зависящих от евклидовой аксиомы параллельности, венгерский математик Янош Бояй назвал «абсолютной» геометрией. Все же остальные теоремы, то есть те, при доказательстве которых мы непосредственно или косвенно основываемся на V постулате, составляет собственно евклидову геометрию.

В курсе 6 класса важнейшими теоремами абсолютной геометрии являются следующие: теорема о смежных и вертикальных углах, о равенстве треугольников, о внешнем угле треугольника, о прямой и ломанной, о сравнительной длине перпендикуляра и наклонных, прямая теорема параллельных.

К собственно евклидовой геометрии относятся: обратная теорема параллельных линиях (то есть о том, что при пересечении двух параллельных прямых третьей соответственные углы равны), теорема о пересечении перпендикуляра и наклонной одной и той же прямой, о сумме углов треугольника со всеми ее следствиями (в том числе и теорема о сумме углов многоугольника).

На аксиоме параллельности основывается почти весь раздел

«Параллелограммы и трапеции». В главе «Об окружности» все теоремы о форме и положении окружности (за исключением теоремы о том, что через всякие три неколлинеарные точки можно провести окружность и следствий этой теоремы). Теорема о зависимости между дугами, хордами и расстояние хорд до центра, о взаимном расположении прямой и окружности не опираются на аксиому параллельных Евклида. Доказательство многих теорем раздела «О вписанных и описанных многоугольниках» существенно основывается на приложении о том, что внешний угол треугольника равен сумме двух внутренних, с ним не смежных углов, а это приложение в свою очередь вытекает из теоремы о сумме углов треугольника – теоремы, непосредственно связанной с евклидовой аксиомой параллельных. Теорема о том, что во всякий треугольник можно вписать окружность, не требует евклидовой аксиомы параллельных.