Аналогично строится модель Клейна геометрии Лобачевского в пространстве, принимая внутренность какого-либо шара за пространство L.

Таким образом, была показана непротиворечивость геометрии Лобачевского. Ее аксиомы и теоремы не могут быть противоречивыми, так как каждой из них соответствует факт евклидовой геометрии внутри круга (или внутри шара). Если в геометрии Лобачевского встретились бы две противоречащие друг другу теоремы, то, переводя эти теоремы на язык обычной геометрии посредством модели Клейна, мы получили бы противоречие между соответствующими теоремами в геометрии Евклида, то есть, построением модели, Клейн показал, что геометрия Лобачевского непротиворечива в такой же мере, в какой непротиворечива геометрия Евклида.

Другую модель геометрии Лобачевского построил в 1882г. французский математик Анри Пуанкаре (1854-1912), применивший ее к решению некоторых важных задач теории функций комплексного переменного.

Одним из важнейших результатов открытия геометрии Лобачевского (называемой также гиперболической геометрией) было развитие новых неевклидовых геометрий, в первую очередь, геометрии Римана (в узком смысле), называемой так же эллиптической геометрией. В качестве модели планиметрии Римана может служить сфера, если считать каждую пару диаметрально противоположных ее точек за одну «точку».

Рис. 11

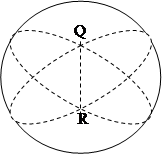
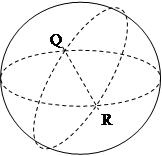Итак, плоскость Римана представлена Евклидовой сферой. На сфере нет прямых линий, но имеются так называемые большие окружности (рис.10), то есть окружности с центром в в центре сферы, которые в качестве геодезических ее линий выполняют на сфере ту же роль, что и прямые на плоскости. Дуги больших окружностей дают кратчайшие расстояния между двумя точками сферы, через которые они проходят, подобно тому, как отрезок прямой на плоскости представляет кратчайшее расстояние между двумя точками сферы, через которую они проходят, подобно тому, как отрезок прямой на плоскости представляет кратчайшее расстояние между его концами; через две точки сферы проходит одна и только одна большая окружность, подобно тому, как две точки плоскости определяют одну и только одну прямую; из дуг больших окружностей на сфере, как из отрезков прямых на плоскости можно образовать сферические треугольники, четырехугольники, многоугольники. Одним словом, большие окружности сферы – это ее «прямые» (рис.11). Однако, наряду с некоторыми сходствами, имеется и большое различие между сферической геометрией с одной стороны и геометрией Евклида и Лобачевского с другой. Аксиомы, следовательно, и теоремы, и формулы сферической геометрии во многом отличаются от аксиом, теорем и формул плоской геометрии Евклида, а так же Лобачевского. В частности, прямые Римана все замкнуты и конечны, имея одну и ту же длину. Сумма углов сферического треугольника, как известно, больше 2d, каждые две прямые имеют одну общую точку, то есть, на римановой плоскости нет параллельных прямых.

В разработку эллиптической геометрии значительный вклад внес Гаусс своими исследованиями о поверхностях.

Сравнивая три, в известном смысле дополняющих друг друга , геометрии: гиперболическую, евклидову (называемую так же параболической) и эллиптическую, следует отметить, что в первой из них через точку вне данной прямой можно провести к этой прямой две параллельные, во второй – одну, а в третей – ни одной. В первой сумма внутренних углов треугольника меньше 2d, во второй равна 2d, а в третей – меньше 2d.

Возникшие из попыток доказательства V постулата неевклидовы геометрии, открытые Лобачевским, Бояй, Гауссом и Риманом и развитые в трудах Бельтрами, Кэли, Клейна, Пуанкаре и других ученых, стали в наши дни необходимым аппаратом для изучения механики, физики и астрономии. Особенно важна геометрия Лобачевского для теории относительности, так как группа важных для теории относительности «преобразований Лоренца» изоморфна группе движений пространства Лобачевского. С другой стороны, открытие неевклидовой геометрии привело к новым исследованиям в области оснований геометрии и, в частности, к аксиоматике Гильберта. Отказываясь от аксиомы Архимеда или от аксиомы Кантора, он получает «неархимедову» соответственно «неканторову» геометрию и т.п.

Открытие неевклидовой геометрии, начало которому положил Лобачевский, не только сыграло огромную роль в развитии новых идей и методов в математике естествознании, но имеет и философское значение. Господствовавшее до Лобачевского мнение о незыблемости геометрии Евклида в значительной мере основывалось на учении известного немецкого философа И. Канта (1724-1804), родоначальника немецкого классического идеализма. Кант утверждал, что человек упорядочивает явления реального мира согласно априорным представлениям, а геометрические представления и идеи якобы априорны (латинское слово aprior означает – изначально, заранее), то есть, не отражают явлений действительного мира, не зависят от практики, от опыта, а являются врожденными человеческому миру, раз и навсегда зафиксированными, свойственными человеческому разуму, его духу. Поэтому , Кант считал, что Евклидова геометрия непоколебима, неизменна, и является вечной истиной. Еще до Канта геометрия Евклида считалась незыблемой, как единственно возможное учение о реальном пространстве.

Открытие неевклидовой геометрии доказало, что нельзя абсолютировать представления о пространстве, что «употребительная» (как назвал Лобачевский геометрию Евклида) геометрия не является единственно возможной, однако это не подорвало незыблемость геометрии Евклида. Итак, в основе геометрии Евклида лежат не априорные, врожденные уму понятия и аксиомы, а такие понятия, которые связаны с деятельностью человека, с человеческой практикой. Только практика может решить вопрос о том, какая геометрия вернее излагает свойства физического пространства. Открытие неевклидовой геометрии дало решающий толчок грандиозному развитию науки, способствовало и поныне способствует более глубокому пониманию окружающего нас материального мира.

Библиография

1. Г.И. Глейзер. История математики в школе IX – X классы. Пособие для учителей. Москва, «Просвещение» 1983г.

2. Даан Дальмедино А., Пейффер И. Пути и лабиринты. Очерки по истории математики. Перевод с французского. М: Мир.1986г.

3. Б.Л. Лаптев. Н.И. Лобачевский и его геометрия. Пособие для учащихся. М. «Просвещение», 1970г.

4. И.М. Яглам. Принцип относительности Галилея и неевклидова геометрия.Серия «Библиотека математического кружка» М: 1963г.