Синтез комбинацонных схем и конечных автоматов, сети Петри

Рефераты >> Программирование и компьютеры >> Синтез комбинацонных схем и конечных автоматов, сети Петри

На основе введённых понятий можно сформулировать ряд свойств сети Петри, характеризующих её в процессе смены маркировок – назовём их поведенческими свойствами сети Петри. Определим наиболее важные из них.

1 Достижимость данной маркировки. Пусть имеется некоторая маркировка μ, отличная от начальной. Тогда возникает вопрос достижимости: можно ли путём запуска определённой поледовательности переходов перейти из начальной в заданную маркировку.

2 Ограниченность. Сеть Петри называется k- ограниченной, если при любой маркировке количество фишек в любой из позиций не превышает k. В частности, сеть называется безопасной, если k равно 1. Кроме того, сеть называется однородной, если в ней отсутствуют петли и одинарной (простой), если в ней нет кратных дуг.

3 Активность. Сеть Петри называется активной, если независимо от дотигнутой из μ0 маркировки существует последовательность запусков, приводящая к запуску этого перехода.

Реально вводят понятия нескольких уровней активности для конкретных переходов. Переход tj T называется:

а) пассивным (L0- активным), если он никогда не может быть запущен;

б) L1- активным, если он может быть запущен последовательностью переходов из μ0 хотя бы один раз;

в) L2- активным, если для любого числа K существует последовательность запусков переходов из μ0 , при которой данный переход может сработать K и более раз;

г) L3- активным, если он является L2- активным при K → ∞.

4 Обратимость. Сеть Петри обратима, если для любой маркировки μ R(C, μ0) маркировка μ0 достижима из μ.

5 Покрываемость. Маркировка μ покрываема, если существует другая маркировка μ’ R(C, μ0) такая, что в каждой позиции μ’ фишек не меньше, чем в позициях маркировки μ.

6 Устойчивость. Сеть Петри называется устойчивой, если для любых двух разрешённых переходов срабатывание одного из них не приводит к запрещению срабатывания другого.

Существуют два основных метода анализа сетей Петри: матричные и основанные на построении дерева покрываемости.

Первая группа методов основана на матричном представлении маркировок и последовательностей запуска переходов. Для этого определим две матрицы размерности количество позиций количество переходов, связанные со структурой сети. Первая матрица называется матрицей входов:

D – [i, j] = # (pi , I(tj)), (3.2.16)

каждый её элемент равен числу фишек, уходящих из j- й позиции при запуске i- го перехода. Вторая матрица называется матрицей выходов:

D + [i, j] = # (pi , O(tj)), (3.2.17)

каждый её элемент равен числу фишек, приходящих в j- ю позицию при запуске i- го перехода. Определим единичный вектор e[j] размерности m, содержащий нули во всех позициях кроме той, которая соответствует запускаемому в данный момент переходу. Очевидно, что переход разрешён, если μ ≥ e[j]·D –. Тогда результат запуска j- го перехода можно описать так:

μ’ = μ + e[j]·D, (3.2.18)

где D = (D + – D –) – матрица изменений. Тогда все сформулированные ранее проблемы сети Петри легко интерпретируются матричными уравнениями вида

μ = μ0 + σ·D, (3.2.19)

где μ – исследуемая маркировка, σ – вектор, компоненты которого показывают, сколько раз срабатывает каждый переход.

Хотя данный метод достаточно прост, он не лишён некоторых недостатков. А именно, его применение даёт лишь необходимые условия существования какого- либо свойства, иными словами, может гарантировать лишь его отсутствие, а о присутствии мы сможем говорить с уверенностью, только проанализировав дерево покрываемости (смены) маркировок.

Дерево маркировок сети – это связанный граф, в вершинах которого находятся маркировки, которых мы достигли в результате последовательного запуска разрешённых переходов, а на дугах, соединяющих вершины – зпускаемые переходы. Путь от корня к каждой маркировке отражает последовательность запусков, приведшую к ней. Корнем дерева является начальная маркировка. При неограниченном накапливании фишек в позиции на дереве образуется петля, а в маркировке на месте, соответствующем зациклившейся позиции, ставится ω – символ бесконечно большого числа.

Ясно, что этот метод хотя и требует утомительного перебора всех возможных маркировок сети, но зато по уже готовому дереву достаточно легко анализировать проблемы достижимости, покрываемости, активности, обратимости сети.

Описав поведенческие свойства и методы анализа, можно перейти непосредственно к анализу конкретной сети Петри.

3.3 Расчёты и полученные результаты

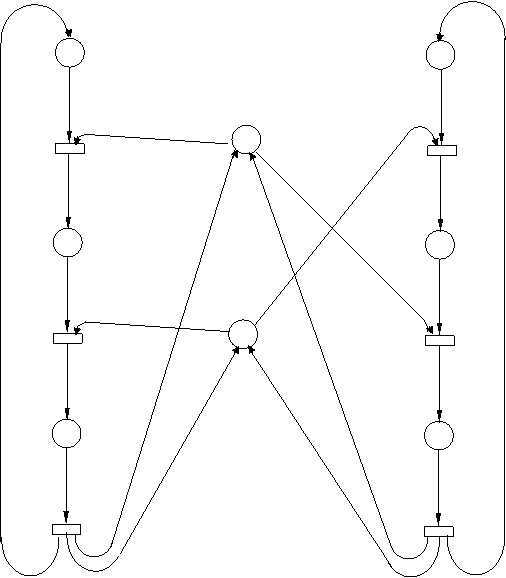
Исходная сеть в виде графа:

p1 p6

▪ ▪

t1 ▪ p4 t4

p2 p7

t2 ▪ p5 t5

p3 p8

t3 t6

Рисунок 3.3.1 – Исходная сеть Петри

Для матричного анализа сети найдём её матрицу изменений.

(3.3.1)

(3.3.2)

Матрицу изменений найдём как разность между (3.3.2) и (3.3.1):

(3.3.3)

Таким образом, получив матрицу изменений, можно записать матричное уравнение смены маркировок вида (3.2.19). Вектор начальной маркировки определим так:

μ0 = (10011100) (3.3.4)

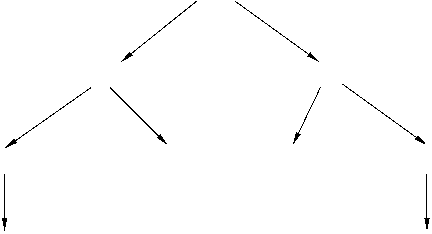
Составим дерево покрываемости маркировок сети.

(10011100) ‘Новая’

t1 t4

‘Новая’ ‘Новая’

(01001100) (10010010)

t2 t4 t1 t5

(00100100) (01000010) (01000010) (10000001)

‘Новая’ ‘Тупик’ ‘Тупик’ ‘Новая’

t3 t6

(10011100) ‘Старая’ (10011100) ‘Старая’

Рисунок 3.3.1 – Дерево покрываемости маркировок

Дерево покрываемости удобно оформить в виде графа. При этом более наглядно видны зацикливающиеся переходы, тупиковые маркировки никакими дополнительными пояснениями снабжать не требуется – отсутствие дуг, исходящих из данной маркировки, говорит само за себя. При достижении старой маркировки её не нужно заново наносить на граф – достаточно соединить дугой предыдущую маркировку и уже существующую “старую”.

Граф покрываемости сети выглядит следующим образом:

μ0

t3 t6

10011100

00100100 t1 t4 10000001

t2 t5

01001100 10010010

t4 t1

01000010

Рисунок 3.3.2 – Граф покрываемости маркировок сети Петри

Проанализируем сеть двумя методами – матричным и графическим и сравним полученные результаты.