Величина в знаменателе правой части (2.29) имеет размер­ность сопротивления, обозначается Хс и называется емкостным со­противлением:

.

Емкостное сопротивление обратно пропорционально частоте и емкости конденсатора.

Таким образом, Im = Um/Xc

Поделив обе части этого уравнения на , получим выражение закона Ома для действующих значений тока и напряжения:

I = U/Xc.

Комплексный ток на основании (2.28)

. (2.30)

С учетом выражения (2.30) можно найти соотношение между комп­лексным напряжением и током в цепи с емкостью:

/

Векторная диаграмма комплексных значений напряжения и тока представлена на рис. 2.18, в.

ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ ПРИ ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ ЭЛЕМЕНТОВ С R, L И С

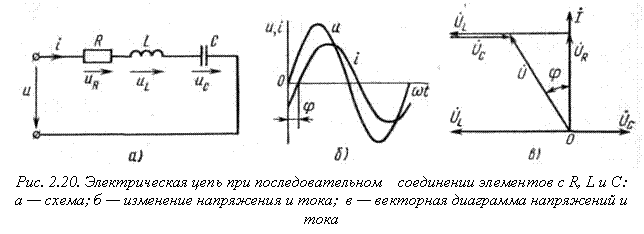Схеме электрической цепи, изображенной на рис. 2.20, а, может соответствовать цепь последовательно соединенных индуктивной ка­тушки с активным сопротивлением R и индуктивностью L и конден­сатора с емкостью С. Активное сопротивление может также соответ­ствовать сопротивлению какого-либо резистора. Во всяком случае, R, L и С — это параметры электрической цепи, причем активное со­противление R характеризует активный (необратимый) процесс пре­образования электрической энергии в другие виды энергии, а индуктивность L и емкость С — обратимый процесс преобразования энер­гии электромагнитного поля.

Под действием напряжения источника питания в цепи возникает ток i. Ток создает падения напряжения на элементах цепи: uR = Ri — на элементе с активным сопротивлением; uL = - еL = L di/dt — на элементе с индуктивностью; — на элементе с емкостью.

По второму закону Кирхгофа для данной цепи запишем

или . (2.31)

В результате решения уравнения (2.31) найдем i(t).

Полным решением линейного дифференциального уравнения (2.31) с постоянными коэффициентами является сумма частного решения этого уравнения и общего решения однородного дифференциального уравнения

. (2.32)

Уравнение (2.32) записано по второму закону Кирхгофа для цепи с последовательным соединением элементов R, L и С, когда напряже­ние источника питания равно нулю, т.е. когда электрическая цепь замкнута накоротко и электрическая энергия извне в цепь не посту­пает. В этих условиях ток в цепи может существовать только за счет запасов энергии в магнитном поле катушки или в электрическом поле конденсатора. При протекании тока через элемент с сопротивлением R происходит преобразование электроэнергии в тепловую и рассеяние ее в окружающую среду. Поэтому через некоторое время запасы элект­роэнергии будут израсходованы. Иными словами, ток, найденный в ре­зультате решения уравнения (2.32), через некоторое время будет ра­вен нулю.

Время, в течение которого существует этот ток, является временем переходного процесса в цепи и обычно исчисляется долями секунды.

Так как на данном этапе нас интересует только установившийся, стабильный, режим цепи, существующий сколь угодно долго, то общего решения уравнения (2.31) искать не будем.

Найдем частное решение уравнения (2.31), т.е. ток установивше­гося режима. Так как правая часть этого уравнения — синусоидаль­ная функция, то и частное решение следует искать в виде синусоидаль­ной функции

. (2.33)

Функция i(t) полностью определена, если известны амплитуда тока Im и угол сдвига фаз между напряжением и током. Найдем эти величины.

Как было показано ранее, напряжение изображается комплексным числом ; ток — комплексным числом ; прои­зводная di/dt — комплексным числом ; интеграл — ком­плексным числом .

Перейдем от дифференциального уравнения (2.31) к алгебраиче­скому уравнению в комплексной форме

.

После преобразований имеем

, (2.34)

а разделив обе части уравнения (2.34) на , получим аналогичное линейное алгебраическое уравнение для комплексных действующих значений:

, (2.35)

Коэффициент

(2.36)

является полным сопротивлением цепи в комплексной форме. Вещест­венная составляющая R полного сопротивления равна активному со­противлению цепи, а мнимая составляющая X называется ее реак­тивным сопротивлением. Реактивное сопротивление цепи равно раз­ности индуктивного и емкостного сопротивлений:

X = XL —ХC .

С учетом (2.36) уравнения (2.34) и (2.35) принимают вид

; ,

откуда комплексное полное сопротивление

(2.37)

где модуль полного сопротивления

. (2.38)

Таким образом, из (2.38) и (2.37) следует, что модуль полного со­противления цепи равен отношению модулей действующих значений напряжения и тока, а аргумент комплексного сопротивления — сдвигу фаз между векторами напряжения и тока.

Модуль полного сопротивления цепи на основании (2.36)

, (2.39)

т.е. полное сопротивление цепи равно корню квадратному из суммы квадратов активного и реактивного сопротивлений.

Итак, из (2.38) можно найти амплитуду тока, определяющую функ­цию i(t) в уравнении (2.33):

.

Теперь, если воспользоваться равенством