Однако при всей значимости результатов, полученных многими чрезвычайно изобретательными математиками XVII столетия исчисления еще не было. Необходимо было выделить общие идеи лежащие в основе решения многих частных задач, а также установить связь операций дифференцирования и интегрирования, дающую достаточно общий алгоритм. Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт, известным под названием формулы Ньютона — Лейбница. Тем самым окончательно оформился общий метод. Предстояло еще научится находить первообразные многих функций, дать логические нового исчисления и т. п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано.

Методы математического анализа активно развивались в следующем столетии (в первую очередь следует назвать имена Л. Эйлера, завершившего систематическое исследование интегрирования элементарных функций, и И. Бернулли). В развитии интегрального исчисления приняли участие русские математики М.В.Остроградский (1801—1862), В.Я.Буняковский (1804—1889), П.Л.Чебышев (1821—1894). Принципиальное значение имели, в частности, результаты Чебышева, доказавшего, что существуют интегралы, не выразимые через элементарные функции.

Строгое изложение теории интеграла появилось только в прошлом веке. Решение этой задачи связано с именами О.Коши, одного из крупнейших математиков, немецкого ученого Б.Римана (1826—1866), французского математика Г.Дарбу (1842—1917).

Ответы на многие вопросы, связанные с существованием площадей и объемов фигур, были получены с созданием К. Жорданом (1838—1922) теории меры.

Различные обобщения понятия интеграла уже в начале нашего столетия были предложены французскими математиками А. Лебегом (1875—1941) и А. Данжуа (1884—1974), советским математиком А. Я. Хинчинчиным (1894—1959).

Определение и свойства интеграла

Если F(x) – одна из первообразных функции f(x) на промежутке J, то первообразная на этом промежутке имеет вид F(x)+C, где CÎR.

Определение. Множество всех первообразных функции f(x) на промежутке J называется определенным интегралом от функции f(x) на этом промежутке и обозначается ò f(x)dx.

ò f(x)dx = F(x)+C, где F(x) – некоторая первообразная на промежутке J.

f ­– подынтегральная функция, f(x) – подынтегральное выражение, x – переменная интегрирования, C – постоянная интегрирования.

Свойства неопределенного интеграла.

1. (ò f(x)dx) ¢ = ò f(x)dx ,

ò f(x)dx = F(x)+C, где F ¢(x) = f(x)

(ò f(x)dx) ¢= (F(x)+C) ¢= f(x)

2. òf¢(x)dx = f(x)+C – из определения.

3. ò k f (x)dx = k ò f¢(x)dx

если k – постоянная и F ¢(x)=f(x),

ò k f (x)dx = k F(x)dx = k(F(x)dx+C1)= k ò f¢(x)dx

4. ò ( f(x)+g(x)+ .+h(x) )dx = ò f(x)dx + ò g(x)dx + .+ ò h(x)dx

ò ( f(x)+g(x)+ .+h(x) )dx = ò [F ¢(x)+G ¢(x)+ .+H ¢(x)]dx =

= ò [F(x)+G(x)+ .+H(x)] ¢dx = F(x)+G(x)+ .+H(x)+C=

= ò f(x)dx + ò g(x)dx + .+ ò h(x)dx, где C=C1+C2+C3+ .+Cn.

Интегрирование

· Табличный способ.

· Способ подстановки.

Если подынтегральная функция не является табличным интегралом, то возможно (не всегда) применить этот способ. Для этого надо:

1. разбить подынтегральную функцию на два множителя;

2. обозначить один из множителей новой переменной;

3. выразить второй множитель через новую переменную;

4. составить интеграл, найти его значение и выполнить обратную подстановку.

Примечание: за новую переменную лучше обозначить ту функцию, которая связана с оставшимся выражением.

Примеры:

1. ò xÖ(3x2–1)dx;

Пусть 3x2–1=t (t³0), возьмем производную от обеих частей:

6xdx = dt

xdx=dt/6

3

ó dt 1 1 ó 1 1 t 2 2 1 ———Ø

ô— t 2 = — ô t 2dt = – ——– + C = —Ö 3x2–1 +C

õ 6 6 õ 6 3 9

2. t

ò sin x cos 3x dx = ò – t3dt = – – + C

4

Пусть cos x = t

-sin x dx = dt

· Метод преобразования подынтегральной функции в сумму или разность:

Примеры :

1. ò sin 3x cos x dx = 1/2ò (sin 4x + sin 2x) dx = 1/8 cos 4x – ¼ cos 2x + C

2.

ó x4+3x2+1 ó 1 1

ô———— dx = ô( x2+2 – ——– ) dx = — x2 + 2x – arctg x + C

õ x2+1 õ x2+1 3

Примечание: при решении этого примера хорошо делать многочлены ”углом”.

· По частям

Если в заданном виде взять интеграл невозможно, а в то же время, очень легко находится первообразная одного множителя и производная другого, то можно использовать формулу.

(u(x)v(x))’=u’(x)v(x)+u(x)v(x)

u’(x)v(x)=(u(x)v(x)+u(x)v’(x)

Проинтегрируем обе части

ò u’(x)v(x)dx=ò (u(x)v(x))’dx – ò u(x)v’(x)dx

ò u’(x)v(x)dx=u(x)v(x)dx – ò u(x)v’(x)dx

Примеры:

1. ò x cos (x) dx = ò x dsin x = x sin x – ò sin x dx = x sin x + cos x + C

x = u(x)

cos x = v’(x)

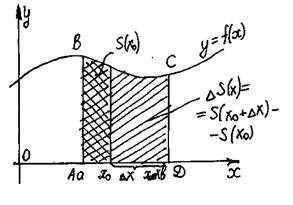
Криволинейная трапеция

Определение. Фигура, ограниченная графиком непрерывной, знакопостоянной функции f(x), осью абцисс и прямыми x=a, x=b, называется криволинейной трапецией.

Способы нахождения площади криволинейной трапеции

I. Теорема. Если f(x) непрерывная и неотрицательная функция на отрезке [a;b], то площадь соответствующей криволинейной трапеции равна приращению первообразных.

Дано: f(x)– непрерывная неопр. функция, xÎ[a;b].

Доказать: S = F(b) – F(a), где F(x) – первообразная f(x).

Доказательство:

2) Докажем, что S(a) – первообразная f(x).

1. D( f ) = D(S) = [a;b]

2. S’(x0)= lim( S(x0+Dx) – S(x0) / Dx ), при Dx®0 DS – прямоугольник

Dx®0 со сторонами Dx и f(x0)

S’(x0) = lim(Dx f(x0) /Dx) = lim f(x0)=f(x0): т.к. x0 точка, то S(x) –

Dx®0 Dx®0 первообразная f(x).

Следовательно по теореме об общем виде первообразной S(x)=F(x)+C.

3) Т.к. S(a)=0, то S(a) = F(a)+C

C = –Fa

4) S = S(b)=F(b)+C = F(b)–F(a)

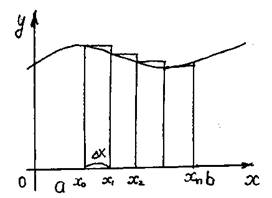
II.