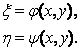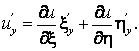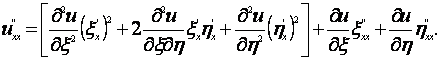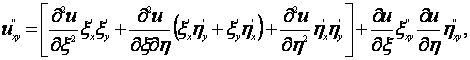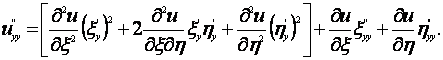Будем рассматривать задачу при следующих условиях. Пусть PC – давление на границе контура питания. При значении радиуса, равном радиусу контура питания

давление поддерживается равным Рс:

Pс – давление на контуре питания.

При значении радиуса, равном радиусу скважины

давление поддерживается равным PW:

где PW – давление в скважине.

1.4. Основные идеи метода характеристик[6]

В данном разделе рассмотрим метод характеристик. Любое линейное дифференциальное уравнение второго порядка (при двух независимых переменных) может быть записано в следующем виде:

где а, b, с, d, e, f, g — заданные непрерывные функции от x и y (или в частном случае, постоянные).

Попытаемся упростить это уравнение с помощью замены независимых переменных:

Здесь x и h — новые независимые переменные. Функции j и y, связывающие новые переменные со старыми, будут подобраны позднее; пока же мы будем считать их дифференцируемыми нужное число раз. Кроме того, будем считать, что система уравнений (1.4.2) может быть однозначно разрешена относительно х и у; это надо понимать следующим образом: если функции j и y и отображают некоторую область G плоскости Оху в область G* плоскости Oxh, то при этом каждой точке (x ,h) области G* соответствует только одна точка области G (иначе говоря, отображение области G на G*, даваемое функциями j и y, является взаимно однозначным). Как известно, для этого достаточно, чтобы якобиан преобразования (т. е. определитель 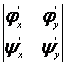) нигде в области G не обращался в нуль.

Для того чтобы сделать требуемую замену переменных, выразим частные производные от функции u по х и у через производные от и по x и h:

Это записано на основании правила дифференцирования сложной функции от двух переменных (здесь u зависит от x и h, которые, в свою очередь, зависят от x и у). Для того чтобы выразить , через производные по x и h, учтем формулу (1.4.31) и применим снова правило дифференцирования сложной функции:

Следовательно,

Аналогично найдем:

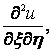
Правые части равенств (1.4.31), (1.4.32), (1.4.41), (1.4.42), (1.4.43) представляют собой линейные функции относительно частных производных , Подставляя u'x, u'y, u'xx, . из этих формул в уравнение (1), мы получим снова линейное уравнение второго порядка с неизвестной функцией и и независимыми переменнымиx и h:

где

a — функция, линейная относительно и’x , u’h , u .

Уравнение (1.4.5) становится особенно простым, если в нем коэффициенты а и с окажутся равными нулю. Для того чтобы первоначально заданное уравнение (1.4.1) можно было привести к такому простому виду, надо в нем сделать замену переменных

подобрав функции j и y так, чтобы они являлись решениями уравнения: