Общая гидродинамика
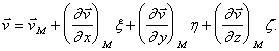(13)
Здесь 
- координаты точки 
относительно точки 
, так что
Введем в рассмотрение матрицу из девяти элементов
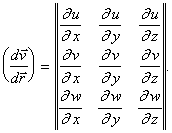
Тогда (13) можно переписать следующим образом:
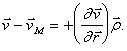
Полученное равенство не зависит от системы координат и в любой системе координат вектору 
ставит в соответствие вектор 
. Это свойство равенства является необходимым и достаточным условием того, что входящая в него матрица 
определяет тензор.
Преобразуем разложение (13) так, чтобы привести его к виду
(14)
В силу линейности (13) по функция 
должна быть квадратичной относительно переменных, и ее можно записать следующим образом:
Спроектируем (14) на оси координат:
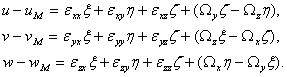(15)
Сравнивая (15) с (13), находим коэффициенты квадратичной формы и проекции векторов 
:
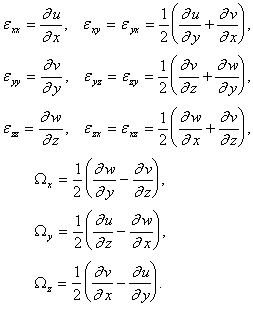(16)
Эти величины определяются единственным образом. Разберем смысл формул (14). Предварительно отметим, что для абсолютно твердого тела имеем 
, где 
- скорость полюса 
- вектор мгновенной угловой скорости, с которой твердое тело вращается относительно мгновенной оси, проходящей через . Из (14) следует, что скорость в некоторой точке сплошной среды складывается из скорости полюса , скорости этой точки во вращательном движении затвердевшей частицы вокруг мгновенной оси, проходящей через полюс , скорости деформации 
. Угловая скорость вращения частицы равна
скорость деформации частицы
На основании соотношений (16) тензор можно представить в виде суммы симметричного и антисимметричного тензоров:
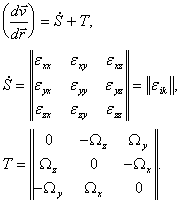(17)
Симметричный тензор 
определяет скорости деформации частицы и называется тензором скоростей деформации. С этим тензором связана симметрическая квадратичная форма 
. Как и в случае тензора напряжений, существуют главные координатные оси 
, в которых квадратичная форма принимает простейшую форму
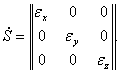
Переход от произвольной системы координат к главным осям осуществляется невырожденным линейным преобразованием. Главные скорости деформации 
находятся как корни векового уравнения
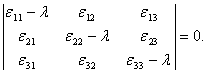
Имеются три инварианта тензора скоростей деформации - линейный 
, квадратичный 
, кубический 
. В частности, для линейного инварианта имеем выражения
(18)
Связь тензоров напряжений и скоростей деформации. Ньютоновская жидкость. Тензоры 
и характеризуют напряжение и деформированное состояние в данной точке сплошной среды. Для конкретной среды должна быть определена связь между этими тензорами. В случае вязкой жидкости такая связь устанавливается законом Навье-Стокса.
В основу модели вязкой жидкости положены следующие предположения:
1. в жидкости наблюдаются только нормальные напряжения, если жидкость покоится или движется как твердое тело;
2. жидкость изотропна - свойства ее одинаковы по всем направлениям;
3. компоненты тензора напряжений есть линейные функции компонент тензора скоростей деформации.
Наиболее общий вид связи между тензорами и , удовлетворяющий этим условиям, есть
(19)
Здесь 
- единичный тензор, 
и 
- скалярные величины. Если движение отсутствует, отсюда получаем 
. Это означает, что в этом случае в жидкости действительно существуют только нормальные напряжения, одинаковые в силу изотропии жидкости. Так как вязкость проявляется лишь при движении, то естественно считать, что напряженное состояние в вязкой жидкости будет таким же, как в покоящейся идеальной жидкости, - на каждой площадке будет действовать по нормали к ней гидростатическое давление 
. Значение выражается через первый инвариант тензора :
Обобщая это соотношение, определим давление в движущейся вязкой жидкости соотношением
