4. Построение оптимальной формы днища

Большой интерес представляет случай оптимального проектирования комбинированных баллонов в форме оболочек вращения, образуемых намоткой армированной ленты на металлическую оболочку. Рассмотрим задачу о выборе рациональной формы комбинированной оболочки, в которой армированный слой образован одним семейством нитей, составляющих с меридианом угол .

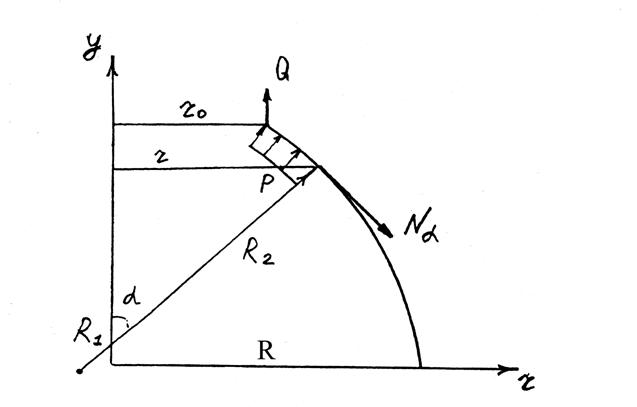
Рис. 2

- внутреннее давление

- главные радиусы кривизны

- осевая сила

Армирование происходит по геодезическим линиям, при действии постоянного давления . Таким образом, намотка рассматриваемой оболочки по геодезическим линиям позволяет получить равно напряженную систему, т. е. Конструкцию минимальной массы.

Опр.: Геодезической называется линия на поверхности, главная нормаль которой совпадает с нормалью к этой поверхности (геодезическая кривизна которой равна нулю)

Свойства:

1. Линия минимальной длины, соединяющая две точки на поверхности.

2. Гибкая нить, лежащая без трения на выпуклой поверхности, принимает при натяжении форму геодезической.

3. Для того чтобы линия была геодезической на поверхности вращения, необходимо и достаточно, чтобы произведение синуса угла, образуемого ей меридианом, на расстоянии от точки до оси вращения, было постоянным (теорема Клеро).

4.

В соответствии с принятыми гипотезами будем предполагать, что напряжения во всех нитях постоянны и равны предельному, т. е.:

,

а напряжения в металлической оболочке равны пределу текучести, т. е.:

Напряжениями в связующем пренебрегаем, считая:

Тогда запишем уравнения равновесия в виде:

;

(2.1)

.

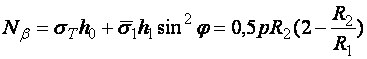Учитывая, что необходимым условием равнопрочности нитяной системы является укладка армирующих элементов по геодезическим линиям поверхности, удовлетворяющим теореме Клеро:

(постоянная определяется через угол намотки на экваторе )

,

и принимая закон изменения толщины композиционного слоя из условия непрерывности намотки

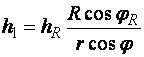
где - толщина спирального слоя и его угол укладки на экваторе баллона.

Главные радиусы кривизны выражаются через уравнения образующей оболочки равенствами:

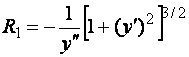
(2.2)

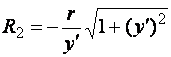
Теперь можно преобразовать уравнения (2.1), получим:

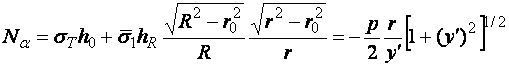
(2.3)

Разделив второе из уравнений на первое и вводя обозначение:

,

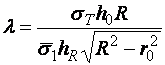получим после некоторых преобразований уравнение, определяющее форму меридиана оптимальной оболочки:

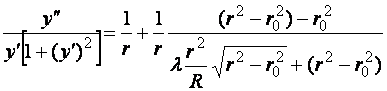. (2.4)

Первый интеграл этого уравнения имеет вид:

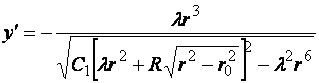
Постоянная может быть определена из условия , что дает:

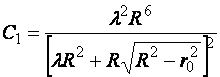
Окончательно форма контура оболочки может быть найдена в результате вычисления следующего интеграла:

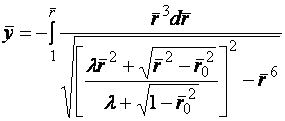, (2.5)

где 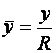, 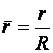- безразмерные координаты, отнесенные к величине радиуса экватора баллона.

Интеграл (2.5) является несобственным при , но его сходимость может быть легко доказана. Соответствующая оценка в районе экватора при будет:

.

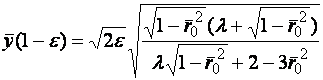Построим график зависимости , который показывает форму контура оптимального комбинированного баллона давления при параметрах .

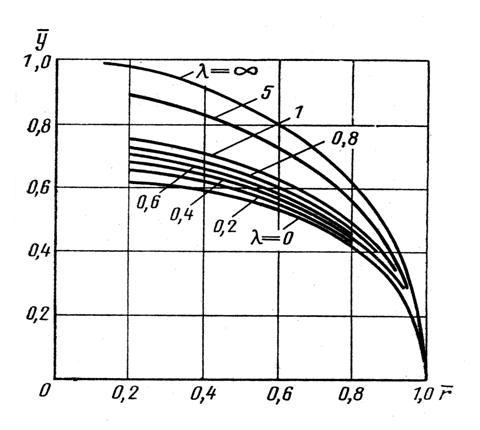
Рис. 3

График зависимости . Формы контуров оптимальных комбинированных баллонов при различных параметрах для .

Найдем безмоментные усилия и и проверим выполнение каждого из уравнений равновесия (2.3). Подставим выражение для образующей (2.5) в правые части равенств (2.3), получим:

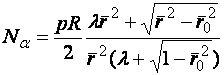
(2.6)

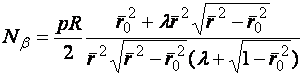
При этом первое из уравнений равновесия (2.3) приводится к виду:

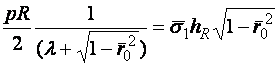
Оно представляет собой условие прочности оболочки на экваторе (при )

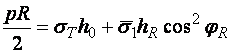. (2.7)