Используя понятия интегральной функции распределения и определенного интеграла можно записать

¦ (x) = F¢ (x) или F (x) = p (x1 < X < x2) = .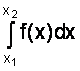

Это соотношение имеет простое геометрическое толкование (рис. 5).

Если 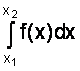определяет заштрихованную область в соответствующих пределах, то

p (х < Х < х + Dх) » ¦ (х) Dх.

Рис. 5. Геометрический смысл дифференциальной функции распределения

Из свойств интегрального распределения следует

.

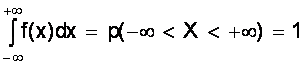Зная дифференциальный закон распределения можно определить интегральный закон распределения

F (x) = .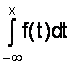

Числовые характеристики случайных величин, заданных своими распределениями

Основными характеристиками случайной величины, заданной своими распределениями, является математическое ожидание ( или среднее значение ) и дисперсия.

Математическое ожидание случайной величины является центром ее распределения. Дисперсия характеризует отклонение случайной величины от ее среднего значения.

Если Х дискретная случайная величина, значения хi которой принимают с вероятностью pi, так, что 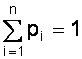, то математическое ожидание М (Х) случайной величины Х определяется равенством

M (X) = ,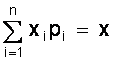

т.е. суммой произведений всех ее возможных значений на соответствующие вероятности.

Математическим ожиданием непрерывной случайной величины является аналог его дискретного выражения

M (X) = .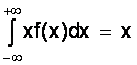

Действительно, все значения в интервале (х; х + Dх) можно считать примерно равными х, а вероятность таких значений равна ¦ (х) dx (см. ранее). Поэтому значения хi дискретного распределения заменяются х, а вероятности pi - на ¦ (х) dx, а сумма заменяется интегралом.

Дисперсией или рассеянием случайной величины Х называется математическое ожидание квадрата разности случайной величины и ее математического ожидания.

D (Х) = М [Х - М (Х)]2 = М (Х - х)2 = s2 (х)

Если случайная величина Х дискретна и принимает значения хi с вероятностями pi, то случайная величина (Х - х)2 принимает значения (хi - х)2 с вероятностями Рi. Поэтому для дискретной случайной величины имеем

D (X) = .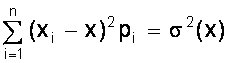

Аналогично для непрерывной случайной величины получаем

D (X) = .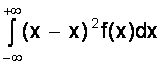

Чем меньше величина дисперсии, тем лучше значения случайной величины характеризуются ее математическим ожиданием.

Основные дискретные и непрерывные законы распределения

Как отмечалось ранее, очень часто случайная величина распределена по нормальному закону. Но существуют и другие распределения, имеющие практическое значение. Рассмотрим некоторые из них по условиям возникновения и основным параметрам их характеризующим.

Равномерное распределение вероятностей.

Пусть плотность вероятности А равна нулю всюду, кроме интервала (a; b), на котором она постоянна (рис. 6). Тогда можно записать

p (a < X < b) = 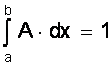A = .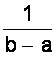

Рис. 6. Дифференциальный и интегральный законы

равномерного распределения

Тогда дифференциальный закон равномерного распределения определяется

¦ (x) =

Интегральный закон распределения

F (x) = .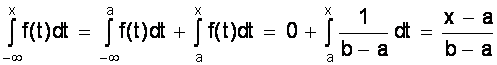

При х ³ b имеем

F (x) =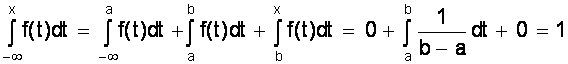

Таким образом интегральный закон равномерного распределения задается (рис. 6)

F (x) =

Основные характеристики распределения

М (X) = ;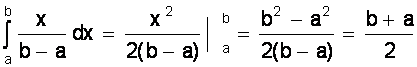

D(X) =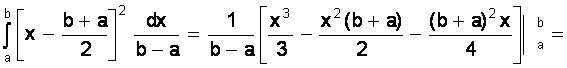

=

=

.

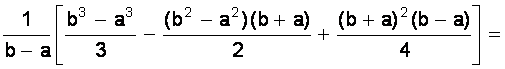
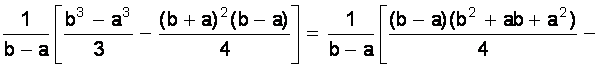
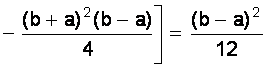Биноминальное распределение

Пусть при некотором испытании событие А может наступить или не произойти (А). Обозначим вероятность А через р, а А через q = 1 -р ( других итогов испытания нет ). Тогда исходами двух последовательных независимых испытаний и их вероятностью будут:

АА - р2; АА - рq; АА - qр; АА - q2.

Отсюда видно, что двукратное появление события А равно р2, вероятность однократного появления - 2 рq, а вероятность того, что А не наступит ни разу - q2. Эти результаты единственно возможные и поэтому

.

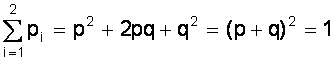Это рассуждение можно перенести на любое число испытаний.

Например, при трех испытаниях получим

.

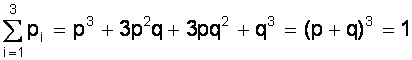Подсчитаем вероятность того, что при n испытаниях событие А появится m раз. Это может произойти, например, в последовательности

Ясно, что вероятность равна рmqn-m. Но m событий А может быть и в другом сочетании. Число всех возможных сочетаний из n элементов по m (количество событий А) равно числу сочетаний . Используя теорему сложения вероятностей получаем общую вероятность Рm,n наступления m событий А из n испытаний

Pm,n =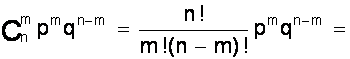

= .

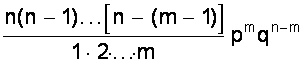Из этой формулы видно, что вероятности Рm,n для различного исхода испытаний (появление или не появление определенного результата А) определяется

pn + npn-1q + .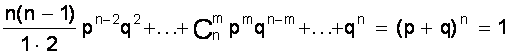

Коэффициенты перед вероятностями р, q являются биноминальными коэффициентами, а общая вероятность представляет слагаемые в разложении бинома ( р + q )n. Поэтому закон распределения случайной величины Х, в котором вероятность наступления событий А определяется коэффициентами бинома, называется биноминальным распределением дискретной случайной величины. Этот закон может быть задан в виде таблицы 1.

Таблица 1

Биноминальный закон распределения